
(本小题满分12分)设某物体一天中的温度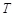 是时间
是时间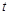 的函数:
的函数: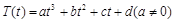 ,其中温度的单位是
,其中温度的单位是 ,时间单位是小时,
,时间单位是小时,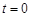 表示12:00,
表示12:00,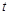 取正值表示12:00以后.若测得该物体在8:00的温度是
取正值表示12:00以后.若测得该物体在8:00的温度是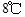 ,12:00的温度为
,12:00的温度为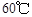 ,13:00的温度为
,13:00的温度为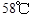 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.
(1)写出该物体的温度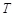 关于时间
关于时间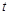 的函数关系式;
的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00和14:00),何时温度最高,并求出最高温度;
(3)如果规定一个函数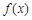 在区间
在区间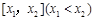 上的平均值为
上的平均值为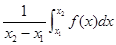 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.
(1)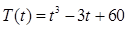 (2)11:00和14:00时,该物体的温度最高,最高温度为
(2)11:00和14:00时,该物体的温度最高,最高温度为 (3)在8:00到16:00这段时间的平均温度为
(3)在8:00到16:00这段时间的平均温度为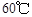
解析试题分析:(1)根据条件,得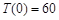 ,
,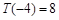 ,
,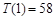 ,
,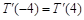 ,
,
可以解得 ,
,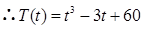 . ……4分
. ……4分
(2)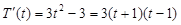 ,
,
当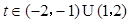 时,
时,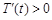 ;
;
当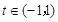 时,
时, .
.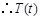 在区间
在区间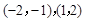 上单调递增,在
上单调递增,在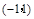 上单调递减,即
上单调递减,即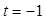 是极大值点.……8分
是极大值点.……8分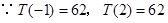 ,
, 在10:00到14:00这段时间中,11:00和14:00时,该物体的温度最高,最高温度为
在10:00到14:00这段时间中,11:00和14:00时,该物体的温度最高,最高温度为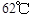 .
.
(3)按规定,平均温度为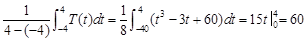 ,
,
即该物体在8:00到16:00这段时间的平均温度为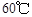 . ……12分
. ……12分
考点:本小题主要考查函数的实际应用、利用导数求最值和定积分的计算,考查学生应用数学知识解决实际问题的能力和由实际问题向数学问题转化的能力以及求解计算能力.
点评:利用导数求解实际生活中的最值问题是高考常考考点,主要是函数模型的建立,对函数解析式的求导,判断单调性,求最值等.问题背景虽然各不相同,但函数模型有限,要总结规律,找出共同的分析思路和一般的解决方法,做到思路清晰,解法成熟,胸有成竹.


科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设平面直角坐标系 中,设二次函数
中,设二次函数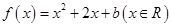 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为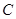 .求:
.求:
(Ⅰ)求实数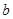 的取值范围;
的取值范围;
(Ⅱ)求圆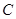 的方程;
的方程;
(Ⅲ)问圆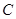 是否经过某定点(其坐标与b 无关)?请证明你的结论.
是否经过某定点(其坐标与b 无关)?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com