
【题目】“若A则B”为真命题,而“若B则C”的逆否命题为真命题,且“若A则B”是“若C则D”的充分条件,而“若D则E”是“若B则C”的充要条件,则¬B是¬E的____条件;A是E的____条件.(填“充分”“必要”、“充要”或“既不充分也不必要”)
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(Ⅰ)求ω的值和f(x)的单调递增区间;
(Ⅱ)若关于x的方程f(x)﹣m=0在区间[0,![]() ]上有两个实数解,求实数m的取值范围.
]上有两个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() 且
且![]() ,在数列
,在数列![]() 中,首项
中,首项![]() ,
,![]() 是其前
是其前![]() 项和,且
项和,且![]() ,
,![]() .
.
(1)设![]() ,
,![]() ,证明数列
,证明数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,证明数列
,证明数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(3)若当且仅当![]() 时,数列
时,数列![]() 取到最小值,求
取到最小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“若A则B”为真命题,而“若B则C”的逆否命题为真命题,且“若A则B”是“若C则D”的充分条件,而“若D则E”是“若B则C”的充要条件,则¬B是¬E的____条件;A是E的____条件.(填“充分”“必要”、“充要”或“既不充分也不必要”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两组各有三名同学,他们在一次测试中的成绩分别为:甲组:88、89、90;乙组:87、88、92.如果分别从甲、乙两组中随机选取一名同学,则这两名同学的成绩之差的绝对值不超过3的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为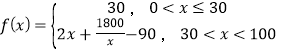 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com