
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 结合图形,逐项分析,得出正确的选项.
解答 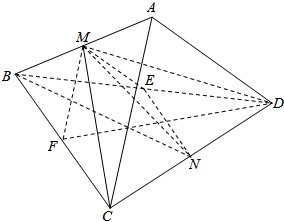 解:(1)连结MC,MD,由三角形三线合一可得AB⊥CM,AB⊥DM,∴AB⊥平面MCD,
解:(1)连结MC,MD,由三角形三线合一可得AB⊥CM,AB⊥DM,∴AB⊥平面MCD,
∵MN?平面MCD,∴AB⊥MN,故(1)正确;
(2)取BD中点E,连结ME,NE,则∠NME为MN与AD所成角,
连结BN,由(1)知BM⊥MN,设正四面体棱长为1,则BM=$\frac{1}{2}$,BN=$\frac{\sqrt{3}}{2}$,∴MN=$\frac{\sqrt{2}}{2}$,
ME=NE=$\frac{1}{2}$,∴cos∠NME=$\frac{M{N}^{2}+M{E}^{2}-N{E}^{2}}{2MN•ME}$=$\frac{\sqrt{2}}{2}$,∴∠NME=45°,故(2)不正确;
(3)由(1)知AB⊥平面CDM,∵AB?平面ABN,∴平面CDM⊥平面ABN,故(3)正确;
(4)取BC早点F,连结MF,DF,假设存在点N,使得过MN的平面与AC垂直,
∴AC⊥MN,∵MF∥AC,∴MF⊥MN,
∵DF=DM=$\frac{\sqrt{3}}{2}$,∴∠FMD<90°,同理,∠CMF<90°.
当N从D向C移动时,∠FMN先减小,后增大,故∠FMN<90°,与MF⊥MN矛盾.
∴不存在点N,使得过MN的平面与AC垂直,故(4)正确.
故选:C.
点评 本题考查了正四面体的结构特征,结合图形构造平面是关键.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
设函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 2 | 5 | |||
| y | 6 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
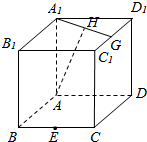 如图,棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D&1的中点,H为A1G的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D&1的中点,H为A1G的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若k=1,则|a-1|<|a-2| | B. | 若k=1,则|a-1|>|a-2| | C. | 若k=2,则|a-1|<|a-2| | D. | 若k=2,则|a-1|>|a-2| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com