
设关于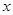 的一元二次方程
的一元二次方程 .
.
(1)若 ,
, 都是从集合
都是从集合 中任取的数字,求方程有实根的概率;
中任取的数字,求方程有实根的概率;
(2)若 是从区间[0,4]中任取的数字,
是从区间[0,4]中任取的数字, 是从区间[1,4]中任取的数字,求方程有实根的概率.
是从区间[1,4]中任取的数字,求方程有实根的概率.
(1)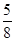 (2)
(2)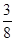
【解析】
试题分析:(1)设事件A=“方程有实根”,记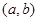 为取到的一种组合,则所有的情况有:
为取到的一种组合,则所有的情况有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4) ……2分
一共16种且每种情况被取到的可能性相同, ……3分
∵关于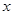 的一元二次方程
的一元二次方程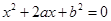 有实根,
有实根,
∴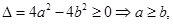 ……4分
……4分
∴事件A包含的基本事件有:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),
(4,2),(4,3),(4,4)共10种, ……5分
 ,
,
∴方程有实根的概率是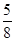 . ……6分
. ……6分
(2)设事件B=“方程有实根”,记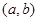 为取到的一种组合,
为取到的一种组合,
∵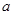 是从区间[0,4]中任取的数字,
是从区间[0,4]中任取的数字,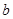 是从区间[1,4]中任取的数字,
是从区间[1,4]中任取的数字,
∴点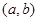 所在区域是长为4,宽为3的矩形区域,如图所示:
所在区域是长为4,宽为3的矩形区域,如图所示:
 ……9分
……9分
又满足: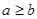 的点的区域是如图所示的阴影部分,
的点的区域是如图所示的阴影部分,
∴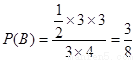 ,
,
∴方程有实根的概率是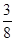 . ……12分
. ……12分
考点:本小题主要考查古典概型和几何概型.
点评:古典概型要求每个基本事件都是等可能发生的,而几何概型包括与长度、面积、体积、角度等有关的几类问题,要正确区分,灵活转化,仔细计算.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:海南省洋浦中学09-10学年高二模块结业考试(数学必修5) 题型:解答题
设关于 的一元二次方程
的一元二次方程





 (
( )有两根
)有两根 和
和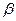 且满足
且满足 .①试用
.①试用 表示
表示 ;②求证:数列
;②求证:数列 是等比数列.
是等比数列.
③当 时,求数列
时,求数列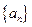 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:云南省芒市中学2011年春季学期期末考试高一年级数学 题型:解答题
(12分)设关于 的一元二次方程
的一元二次方程 ,若
,若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
查看答案和解析>>
科目:高中数学 来源:云南省芒市2011年春季学期期末考试高一年级数学 题型:解答题
(12分)设关于 的一元二次方程
的一元二次方程 ,若
,若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com