
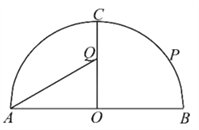
【题目】如图,某景区内有一半圆形花圃,其直径![]() 为
为![]() ,
,![]() 是圆心,且
是圆心,且![]() .在
.在![]() 上有一座观赏亭
上有一座观赏亭![]() ,其中
,其中![]() .计划在
.计划在![]() 上再建一座观赏亭
上再建一座观赏亭![]() ,记
,记![]() .
.
(1)当![]() 时,求
时,求![]() 的大小;
的大小;
(2)当![]() 越大,游客在观赏亭
越大,游客在观赏亭![]() 处的观赏效果越佳,求游客在观赏亭
处的观赏效果越佳,求游客在观赏亭![]() 处的观赏效果最佳时,角
处的观赏效果最佳时,角![]() 的正弦值.
的正弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知向量![]() ,向量
,向量![]() ,且函数
,且函数![]() .
.
(1)求函数![]() 的单调递增区间及其对称中心;
的单调递增区间及其对称中心;
(2)在![]() 中,角A,B,C所对的边分别为a,b,c且角A满足
中,角A,B,C所对的边分别为a,b,c且角A满足![]() .若
.若![]() ,BC边上的中线长为3,求
,BC边上的中线长为3,求![]() 的面积S.
的面积S.
(3)将函数![]() 的图像向左平移
的图像向左平移![]() 个长度单位,向下平移
个长度单位,向下平移![]() 个长度单位,再横坐标不变,纵坐标缩短为原来的
个长度单位,再横坐标不变,纵坐标缩短为原来的![]() 后得到函数
后得到函数![]() 的图像,令函数
的图像,令函数![]() 在
在![]() 的最小值为
的最小值为![]() ,求正实数
,求正实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年国际乒联总决赛在韩国仁川举行,比赛时间为12月13﹣12月16日,在男子单打项目,中国队准备选派4人参加.已知国家一线队共6名队员,二线队共4名队员.
(1)求恰好有3名国家一线队队员参加比赛的概率;
(2)设随机变量![]() 表示参加比赛的国家二线队队员的人数,求
表示参加比赛的国家二线队队员的人数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种体育比赛的规则是:进攻队员与防守队员均在安全线![]() 的垂线
的垂线![]() 上(
上(![]() 为垂足),且分别位于距
为垂足),且分别位于距![]() 为
为![]() 和
和![]() 的点
的点![]() 和点
和点![]() 处,进攻队员沿直线
处,进攻队员沿直线![]() 向安全线跑动,防守队员沿直线方向拦截,设
向安全线跑动,防守队员沿直线方向拦截,设![]() 和
和![]() 交于点
交于点![]() ,若在
,若在![]() 点,防守队员比进攻队员先到或同时到,则进攻队员失败,已知进攻队员速度是防守队员速度的两倍,且他们双方速度不变,问进攻队员的路线
点,防守队员比进攻队员先到或同时到,则进攻队员失败,已知进攻队员速度是防守队员速度的两倍,且他们双方速度不变,问进攻队员的路线![]() 应为什么方向才能取胜?
应为什么方向才能取胜?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C: ![]() ,直线l过点
,直线l过点![]() .
.

(1)若直线l与圆心C的距离为1,求直线l的方程;
(2)若直线l与圆C交于M,N两点,且![]() ,求以MN为直径的圆的方程;
,求以MN为直径的圆的方程;
(3)设直线![]() 与圆C交于A,B两点,是否存在实数a,使得直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,说明理由.
与圆C交于A,B两点,是否存在实数a,使得直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
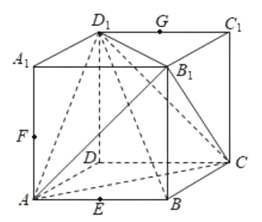
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com