
已知函数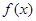 的定义域为R,其导函数
的定义域为R,其导函数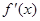 的图像如图所示,则对于任意
的图像如图所示,则对于任意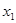 ,
,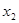
 (
(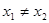 ),下列结论正确的是( )
),下列结论正确的是( )
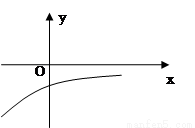
①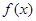 <0恒成立 ②
<0恒成立 ②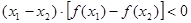 ;③
;③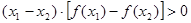 ;
;
④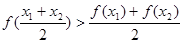 ;⑤
;⑤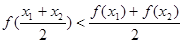 。
。
A.①③ B.①③④ C.②④ D.②⑤
D
【解析】
试题分析:由导函数的图象可知,导函数f′(x)的图象在x轴下方,即f′(x)<0,故原函数为减函数,并且是,递减的速度是先快后慢.由此可得函数f(x)的图象,再结合函数图象易得正确答案.
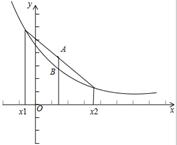
解:由导函数的图象可知,导函数f′(x)的图象在x轴下方,即f′(x)<0,故原函数为减函数,并且是,递减的速度是先快后慢.所以f(x)的图象如图所示. f(x)<0恒成立,没有依据,故①不正确;②表示(x1-x2)与[f(x1)-f(x2)]异号,即f(x)为减函数.故②正确;③表示(x1-x2)与[f(x1)-f(x2)]同号,即f(x)为增函数.故③不正确,④⑤左边边的式子意义为x1,x2中点对应的函数值,即图中点B的纵坐标值,右边式子代表的是函数值得平均值,即图中点A的纵坐标值,显然有左边小于右边,故④不正确,⑤正确,综上,正确的结论为②⑤.故选D.
考点:导数的运用
点评:本题为导函数的应用,由导函数的图象推出原函数应具备的性质,利用数形结合是解决问题的关键,属基础题.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2010年浙江省温州中学高二下学期期中考试数学(文) 题型:解答题
已知函数 的定义域为R,且当
的定义域为R,且当 时,
时, 恒成立,
恒成立,
(1)求证: 的图象关于点
的图象关于点 对称;
对称;
(2)求函数 图象的一个对称点。
图象的一个对称点。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省聊城市高三下学期期初考试文科数学试卷(解析版) 题型:选择题
已知函数 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且
( N*),则
N*),则 的值为( )
的值为( )
A.4024 B.4023 C.4022 D.4021
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三10月月考理科数学卷 题型:选择题
已知函数 的定义域为R,它的反函数为
的定义域为R,它的反函数为 ,如果
,如果 与
与 互为反函数,且
互为反函数,且 ,则
,则 的值为(
)
的值为(
)
A、 B、0
C、
B、0
C、 D、
D、
查看答案和解析>>
科目:高中数学 来源:2012届雅安中学高二第二学期期中考试数学试题 题型:选择题
已知函数 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且 (
( N*),则
N*),则 的值为( )
的值为( )
A. 4016 B.4017 C.4018 D.4019
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com