
【题目】以下四个命题:①两个随机变量的线性相关性越强,相关系数的绝对值越接近1;②在回归分析中,可用相关指数![]() 的值判断拟合效果,
的值判断拟合效果,![]() 越小,模型的拟合效果越好; ③若数据
越小,模型的拟合效果越好; ③若数据![]() 的方差为1,则
的方差为1,则![]() 的方差为4;④已知一组具有线性相关关系的数据
的方差为4;④已知一组具有线性相关关系的数据![]() ,其线性回归方程
,其线性回归方程![]() ,则“
,则“![]() 满足线性回归方程
满足线性回归方程![]() ”是“
”是“![]() ,
,![]() ”的充要条件;其中真命题的个数为( )
”的充要条件;其中真命题的个数为( )
A.4B.3C.2D.1
【答案】C
【解析】
①根据线性相关性与r的关系进行判断,
②根据相关指数![]() 的值的性质进行判断,
的值的性质进行判断,
③根据方差关系进行判断,
④根据点![]() 满足回归直线方程,但点
满足回归直线方程,但点![]() 不一定就是这一组数据的中心点,而回归直线必过样本中心点,可进行判断.
不一定就是这一组数据的中心点,而回归直线必过样本中心点,可进行判断.
①若两个随机变量的线性相关性越强,则相关系数r的绝对值越接近于1,故①正确;
②用相关指数![]() 的值判断模型的拟合效果,
的值判断模型的拟合效果,![]() 越大,模型的拟合效果越好,故②错误;
越大,模型的拟合效果越好,故②错误;
③若统计数据![]() 的方差为1,则
的方差为1,则![]() 的方差为
的方差为![]() ,故③正确;
,故③正确;
④因为点![]() 满足回归直线方程,但点
满足回归直线方程,但点![]() 不一定就是这一组数据的中心点,即
不一定就是这一组数据的中心点,即![]() ,
,![]() 不一定成立,而回归直线必过样本中心点,所以当
不一定成立,而回归直线必过样本中心点,所以当![]() ,
,![]() 时,点
时,点 ![]() 必满足线性回归方程
必满足线性回归方程 ![]() ;因此“
;因此“![]() 满足线性回归方程
满足线性回归方程![]() ”是“
”是“![]() ,
,![]() ”必要不充分条件.故 ④错误;所以正确的命题有①③.
”必要不充分条件.故 ④错误;所以正确的命题有①③.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了使房价回归到收入可支撑的水平,让全体人民住有所居,近年来全国各一、二线城市打击投机购房,陆续出台了住房限购令.某市一小区为了进一步了解已购房民众对市政府岀台楼市限购令的认同情况,随机抽取了本小区50户住户进行调查,各户人平均月收入(单位:千元)的户数频率分布直方图如图,其中赞成限购的户数如下表:
人平均月收入 |
|
|
|
|
|
|
赞成户数 | 4 | 9 | 12 | 6 | 3 | 1 |
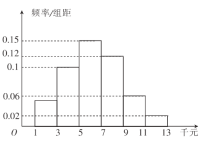
(1)若从人平均月收入在![]() 的住户中再随机抽取两户,求所抽取的两户至少有一户赞成楼市限购令的概率;
的住户中再随机抽取两户,求所抽取的两户至少有一户赞成楼市限购令的概率;
(2)若将小区人平均月收入不低于7千元的住户称为“高收入户”,人平均月收入低于7千元的住户称为“非高收入户”根据已知条件完成如图所给的![]() 列联表,并说明能否有
列联表,并说明能否有![]() 的把握认为“收入的高低”与“赞成楼市限购令”有关.
的把握认为“收入的高低”与“赞成楼市限购令”有关.
非高收入户 | 高收入户 | ||
赞成 | |||
不赞成 | |||
总计 |
附:临界值表
| 0.1 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.63.5 | 10.828 |
参考公式: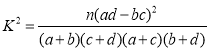 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() 的左、右焦点,直线
的左、右焦点,直线![]() ,将线段
,将线段![]() ,
,![]() 分成两段,其长度之比为
分成两段,其长度之比为![]() ,设
,设![]() 是
是![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为圆
为圆![]() 上一动点,圆心
上一动点,圆心![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的点,且
上的点,且![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 只有一个公共点
只有一个公共点![]() ,且点
,且点![]() 在第二象限,过坐标原点
在第二象限,过坐标原点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C分别为△ABC的三边a,b,c所对的角,向量![]() =(sin A,sin B),
=(sin A,sin B),![]() =(cos B,cos A),且
=(cos B,cos A),且![]() =sin 2C.
=sin 2C.
(1)求角C的大小;
(2)若sin A,sin C,sin B成等差数列,且![]() ,求边c的长.
,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
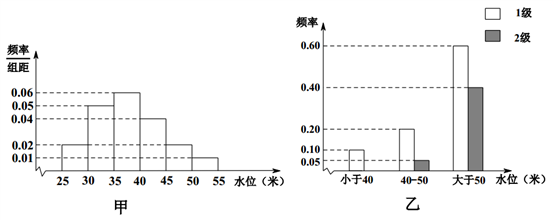
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
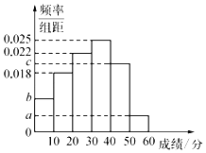
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: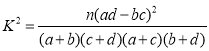 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com