
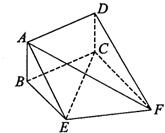
 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF-90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF-90°,BE∥CF,CE⊥EF,AD= ,EF=2.
,EF=2. ,
, ,
, ,得3+(b-c)2=4,∴b-c=-1.
,得3+(b-c)2=4,∴b-c=-1. .
. ,
, 为平面AEF的法向量,则
为平面AEF的法向量,则 ,
, 结合
结合 ,
, .(8分)
.(8分) ,
, ,
, .
. 时,二面角A-EF-C的大小为45°.
时,二面角A-EF-C的大小为45°. ,即可求出向量
,即可求出向量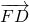 ,然后利用异面直线所在的向量的夹角公式求出所成角即可求得异面直线AD与EF所成角;
,然后利用异面直线所在的向量的夹角公式求出所成角即可求得异面直线AD与EF所成角; ,利用向量的夹角公式求出两向量的夹角,根据二面角平面角的大小建立等式,即可求出此时AB的长.
,利用向量的夹角公式求出两向量的夹角,根据二面角平面角的大小建立等式,即可求出此时AB的长.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
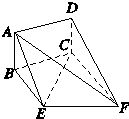 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=
如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=| π |
| 2 |
| 3 |
| CF |
| CD |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,AD=
如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,AD=| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com