
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为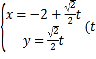 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
【答案】(1)4;(2)16.
【解析】
(1)根据题意,将曲线C的极坐标方程变形为标准方程,将直线的参数方程与曲线C的方程联立,可得![]() ,由一元二次方程根与系数的关系计算可得答案;
,由一元二次方程根与系数的关系计算可得答案;
(2)写出曲线C的参数方程,分析可得以P为顶点的内接矩形周长l![]() ,由正弦函数的性质分析可得答案.
,由正弦函数的性质分析可得答案.
(1)由![]() ,将x=ρcosθ,y=ρsinθ代入得到
,将x=ρcosθ,y=ρsinθ代入得到![]() +3
+3![]() =12,
=12,
所以曲线C的直角坐标方程为![]() +3
+3![]() =12,
=12,![]() 的极坐标为
的极坐标为![]() ,化为直角坐标为(-2,0)
,化为直角坐标为(-2,0)
由直线l的参数方程为: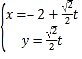 (t为参数),
(t为参数),
知直线l是过点P(-2,0),且倾斜角为![]() 的直线,
的直线,
把直线的参数方程代入曲线C得,![]() .
.
所以|PM||PN|=|t1t2|=4.
(2)由曲线C的方程为 ![]() ,
,
不妨设曲线C上的动点![]() ,
,
则以P为顶点的内接矩形周长l![]() ,
,
又由sin(θ![]() )≤1,则l≤16;
)≤1,则l≤16;
因此该内接矩形周长的最大值为16.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】下列说法中正确的有______
①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响;
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大
③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越准确.
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:①“若x2+ y2 ≠0,则x,y不全为零”的否命题;②“正多边形都相似”的逆命题;③“若m>0,则x2+x-m=0有实根”的逆否命题;其中真命题的序号是____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】配速是马拉松运动中常使用的一个概念,是速度的一种,是指每公里所需要的时间,相比配速,把心率控制在一个合理水平是安全理性跑马拉松的一个重要策略.图1是一个马拉松跑者的心率![]() (单位:次/分钟)和配速
(单位:次/分钟)和配速![]() (单位:分钟/公里)的散点图,图2是一次马拉松比赛(全程约42公里)前3000名跑者成绩(单位:分钟)的频率分布直方图:
(单位:分钟/公里)的散点图,图2是一次马拉松比赛(全程约42公里)前3000名跑者成绩(单位:分钟)的频率分布直方图:
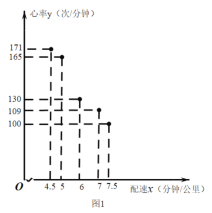
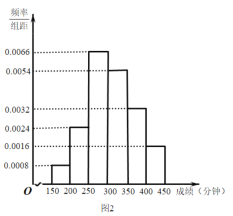
(1)由散点图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 与
与![]() 的线性回归方程;
的线性回归方程;
(2)该跑者如果参加本次比赛,将心率控制在160左右跑完全程,估计他能获得的名次.
参考公式:线性回归方程![]() 中,
中,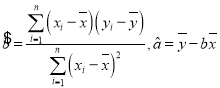 ,参考数据:
,参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M的轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交曲线C于不同于N的两点A,B,直线NA,NB的斜率分别为k1,k2,求k1+k2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com