练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设A，B是治疗同一种疾病的两种药，用若干试验组进行对比试验．每个试验组由4只小白鼠组成，其中2只服用A，另2只服用B，然后观察疗效．若在一个试验组中，服用A有效的小白鼠的只数比服用B有效的只数多，就称该试验组为甲类组．设每只小白鼠服用A有效的概率为，服用B有效的概率为.
    (1)求一个试验组为甲类组的概率；
    (2)观察三个试验组，用X表示这三个试验组中甲类组的个数，求X的分布列和数学期望．

    (1)   (2) X的分布列为

    X
    		0
    		1
    		2
    		3
    P




    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    一个口袋装有n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸2个球(每次摸奖后放回),2个球颜色不同则为中奖.
    (1)试用n表示一次摸奖中奖的概率.
    (2)若n=5,求3次摸奖的中奖次数ξ=1的概率及数学期望.
    (3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某市质监部门对市场上奶粉进行质量抽检，现将9个进口品牌奶粉的样品编号为1，2，3，4， ，9；6个国产品牌奶粉的样品编号为10，11，12，15，按进口品牌及国产品牌分层进行分层抽样，从其中抽取5个样品进行首轮检验，用表示编号为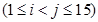的样品首轮同时被抽到的概率．
    （1）求的值；
    （2）求所有的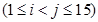的和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某高校在202年自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)， 第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．

    （1）分别求第3，4，5组的频率；
    （2）若该校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，
    (ⅰ)已知学生甲和学生乙的成绩均在第三组，求学生甲和学生乙同时进入第二轮面试的概率；
    (ⅱ)学校决定在这6名学生中随机抽取2名学生接受考官D的面试，设第4组中有名学生被考官D面试，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：

    品牌
    		甲
    		乙
    首次出现故
    障时间x(年)
    		0<x≤1
    		1<x≤2
    		x>2
    		0<x≤2
    		x>2
    轿车数量(辆)
    		2
    		3
    		45
    		5
    		45
    每辆利润
    (万元)
    		1
    		2
    		3
    		1.8
    		2.9
    将频率视为概率，解答下列问题：
    (1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率．
    (2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列．
    (3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.

    （1）求甲一次游戏中能中奖的概率;
    （2）设这个正六边形的面积是6,求一次游戏中随机变量S的分布列及期望值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某小组共有A、B、C、D、E五位同学，他们的身高(单位：m)以及体重指标(单位：kg/m2)如下表所示：

     
    		A
    		B
    		C
    		D
    		E
    身高
    		1.69
    		1.73
    		1.75
    		1.79
    		1.82
    体重指标
    		19.2
    		25.1
    		18.5
    		23.3
    		20.9
     (1)从该小组身高低于1.80的同学中任选2人，求选到的2人身高都在1.78以下的概率；
    (2)从该小组同学中任选2人，求选到的2人的身高都在1.70以上且体重指标都在[18.5，23.9)中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    一投掷飞碟的游戏中，飞碟投入红袋记2分，投入蓝袋记1分，未投入袋记0分．经过多次试验，某人投掷100个飞碟有50个入红袋，25个入蓝袋，其余不能入袋．
    (1)求该人在4次投掷中恰有三次投入红袋的概率；
    (2)求该人两次投掷后得分ξ的数学期望Eξ.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某商场为吸引顾客消费推出一项促销活动，促销规则如下：到该商场购物消费满100元就可转动如图所示的转盘一次，进行抽奖(转盘为十二等分的圆盘)，满200元转两次，以此类推；在转动过程中，假定指针停在转盘的任一位置都是等可能的；若转盘的指针落在A区域，则顾客中一等奖，获得10元奖金；若转盘落在B区域或C区域，则顾客中二等奖，获得5元奖金；若转盘指针落在其他区域，则不中奖(若指针停到两区间的实线处，则重新转动)．若顾客在一次消费中多次中奖，则对其奖励进行累加．已知顾客甲到该商场购物消费了268元，并按照规则参与了促销活动．

    (1)求顾客甲中一等奖的概率；
    (2)记X为顾客甲所得的奖金数，求X的分布列及其数学期望．

    查看答案和解析>>

    同步练习册答案