
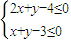
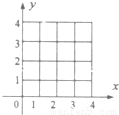
 画出可行域;
画出可行域;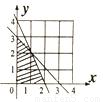 解:(1)不等式组
解:(1)不等式组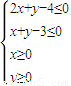 所表示的平面区域,如下图示:
所表示的平面区域,如下图示: ×(3+2)×1+
×(3+2)×1+ ×2×1=
×2×1=
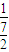 =
= .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:
 (2012•江苏二模)选做题
(2012•江苏二模)选做题| PC |
| PA |
| BD |
| DC |
|
| x2 |
| 16 |
| y2 |
| 9 |
| 13 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•烟台二模)设非负实数x、y满足不等式组
(2009•烟台二模)设非负实数x、y满足不等式组
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省桐乡市高三模拟考试(2月)文科数学试卷(解析版) 题型:选择题
设非负实数x,y满足约束条件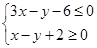 , 若目标函数z=ax+by(a>0,b>0)的最大值为12,则
, 若目标函数z=ax+by(a>0,b>0)的最大值为12,则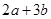 的值为
的值为
A.12 B.26 C.24 D.6
查看答案和解析>>
科目:高中数学 来源:2012年江苏省苏锡常镇四市高考数学二模试卷(解析版) 题型:解答题
 .
.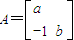 把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.
把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值. =1上的点P到直线l:3x+4y+18=0的距离的最小值.
=1上的点P到直线l:3x+4y+18=0的距离的最小值.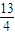 ,求x+y+z的最大值.
,求x+y+z的最大值.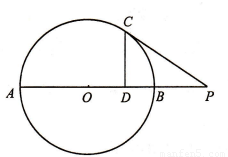
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com