
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2![]() 。
。
(1)求椭圆的方程;
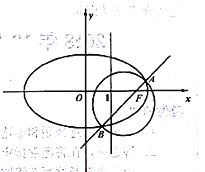
(2)如图,斜率为k的直线l过椭圆的右焦点F,且与椭圆交与A,B两点,以线段AB为直径的圆截直线x=1所得的弦的长度为![]() ,求直线l的方程。
,求直线l的方程。
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)若函数![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了提高职工的健身意识,鼓励大家加入健步运动,要求200名职工每天晚上9:30上传手机计步截图,对于步数超过10000的予以奖励.图1为甲乙两名职工在某一星期内的运动步数统计图,图2为根据这星期内某一天全体职工的运动步数做出的频率分布直方图.
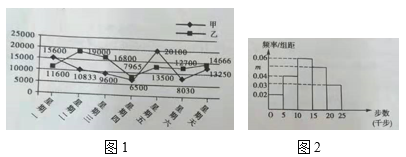
(1)在这一周内任选两天检查,求甲乙两人两天全部获奖的概率;
(2)请根据频率分布直方图,求出该天运动步数不少于15000的人数,并估计全体职工在该天的平均步数;
(3)如果当天甲的排名为第130名,乙的排名为第40名,试判断做出的是星期几的频率分布直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满![]() 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有
元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有![]() 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励
只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励![]() 元;共两只球都是绿色,则奖励
元;共两只球都是绿色,则奖励![]() 元;若两只球颜色不同,则不奖励.
元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得![]() 元的概率;
元的概率;
(2)记![]() 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量
为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其焦点与双曲线
,其焦点与双曲线![]() 的焦点重合,且椭圆
的焦点重合,且椭圆![]() 的短轴的两个端点与其一个焦点构成正三角形.
的短轴的两个端点与其一个焦点构成正三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)过双曲线![]() 的右顶点
的右顶点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .设
.设![]() ,当
,当![]() 为定值时,求
为定值时,求![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后得到函数
个单位后得到函数![]() 的图象,则( )
的图象,则( )
A. ![]() 图象关于直线
图象关于直线![]() 对称 B.
对称 B. ![]() 图象关于点
图象关于点![]() 中心对称
中心对称
C. ![]() 在区间
在区间![]() 单调递增 D.
单调递增 D. ![]() 在区间
在区间![]() 上单调递减
上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a∈R,e为自然对数的底数),
(a∈R,e为自然对数的底数),![]() ,其中
,其中![]() 在x=0处的切线方程为y=bx.
在x=0处的切线方程为y=bx.
(1)求a,b的值;
(2)求证:![]() ;
;
(3)求证:![]() 有且仅有两个零点.
有且仅有两个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ).在以
).在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点.当
两点.当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(Ⅰ)求![]() ,
,![]() 的值及曲线
的值及曲线![]() 和
和![]() 极坐标方程;
极坐标方程;
(Ⅱ)求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 稿酬所得以个人每次取得的收入,定额或定率减除规定费用后的余额为应纳税所得额,每次收入不超过4000元,定额减除费用800元;每次收入在4000元以上的,定率减除20%的费用.适用20%的比例税率,并按规定对应纳税额减征30%,计算公式为:
(1)每次收入不超过4000元的:应纳税额=(每次收入额-800)×20%×(1-30%)
(2)每次收入在4000元以上的:应纳税额=每次收入额×(1-20%)×20%×(1-30%).已知某人出版一份书稿,共纳税280元,这个人应得稿费(扣税前)为 元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com