
【题目】如图,正方体![]() 中,E为AB中点,F在线段
中,E为AB中点,F在线段![]() 上.给出下列判断:①存在点F使得
上.给出下列判断:①存在点F使得![]() 平面
平面![]() ;②在平面
;②在平面![]() 内总存在与平面
内总存在与平面![]() 平行的直线;③平面
平行的直线;③平面![]() 与平面ABCD所成的二面角(锐角)的大小与点F的位置无关;④三棱锥
与平面ABCD所成的二面角(锐角)的大小与点F的位置无关;④三棱锥![]() 的体积与点F的位置无关.其中正确判断的有( )
的体积与点F的位置无关.其中正确判断的有( )
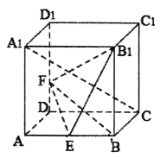
A.①②B.③④C.①③D.②④
【答案】D
【解析】
运用线面垂直的定义,结合反证法即可判断①;运用线面平行的判定定理,即可判断②;由二面角的平面角的定义,结合向量法即可判断③;由线面平行,结合三棱锥的体积公式可以判断④.
对于①,假设存在F使得![]() ⊥平面
⊥平面![]() ,则
,则![]() ⊥
⊥![]() ,又
,又![]() ⊥
⊥![]() ,
,![]() ∩
∩![]() =
=![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ,则
,则![]() ⊥
⊥![]() ,这与
,这与![]() ⊥
⊥![]() 矛盾,所以①错误;
矛盾,所以①错误;
对于②,因为平面![]() 与平面
与平面![]() 相交,设交线为
相交,设交线为![]() ,则在平面
,则在平面![]() 内与
内与![]() 平行的直线平行于平面
平行的直线平行于平面![]() ,故②正确;
,故②正确;
对于③,以![]() 点为坐标原点,以
点为坐标原点,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间坐标系,则平面
轴,建立空间坐标系,则平面![]() 的法向量为
的法向量为![]() 而平面
而平面![]() 的法向量
的法向量![]() ,随着
,随着![]() 位置变化,故平面
位置变化,故平面![]() 与平面
与平面![]() 所成的二面角(锐角)的大小与点
所成的二面角(锐角)的大小与点![]() 的位置有关,故③错误;
的位置有关,故③错误;
对于④,三棱锥![]() 的体积即为三棱锥
的体积即为三棱锥![]() ,因为
,因为![]() ∥平面
∥平面![]() ,所以,当
,所以,当![]() 在线段
在线段![]() 上移动时,
上移动时,![]() 到平面
到平面![]() 的距离不变,故三棱锥
的距离不变,故三棱锥![]() 的体积与点
的体积与点![]() 的位置无关,即④正确.
的位置无关,即④正确.
故选:D.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)不过原点![]() 的直线与椭圆
的直线与椭圆![]() 交于两点
交于两点![]() 、
、![]() ,且直线
,且直线![]() 、
、![]() 、
、![]() 的斜率依次成等比数列,问:直线是否定向的,请说明理由.
的斜率依次成等比数列,问:直线是否定向的,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的一个顶点为![]() ,焦点在x轴上,若右焦点到直线
,焦点在x轴上,若右焦点到直线![]() 的距离为3.
的距离为3.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设椭圆C与直线
设椭圆C与直线![]() 相交于不同的两点M,N,线段MN的中点为E.
相交于不同的两点M,N,线段MN的中点为E.
![]() 当
当![]() 时,射线OE交直线
时,射线OE交直线![]() 于点
于点![]() 为坐标原点
为坐标原点![]() ,求
,求![]() 的最小值;
的最小值;
![]() 当
当![]() ,且
,且![]() 时,求m的取值范围.
时,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学随机抽取部分高一学生调査其每日自主安排学习的时间(单位:分钟),并将所得数据绘制成如图所示的频率分布直方图,其中自主安排学习时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
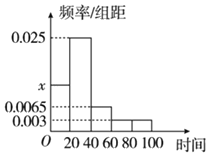
(1)求直方图中x的值;
(2)现采用分层抽样的方式从每日自主安排学习时间不超过40分钟的学生中随机抽取6人,若从这6人中随机抽取2人进行详细的每日时间安排调查,求抽到的2人每日自主安排学习时间均不低于20分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若X是一个集合,![]() 是一个以X的某些子集为元素的集合,且满足:①X属于
是一个以X的某些子集为元素的集合,且满足:①X属于![]() ,
,![]() 属于
属于![]() ;②
;②![]() 中任意多个元素的并集属于
中任意多个元素的并集属于![]() ;③
;③![]() 中任意多个元素的交集属于
中任意多个元素的交集属于![]() .则称
.则称![]() 是集合X上的一个拓扑.已知集合
是集合X上的一个拓扑.已知集合![]() ,对于下面给出的四个集合
,对于下面给出的四个集合![]() :
:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中是集合X上的拓扑的集合![]() 的序号是________.
的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com