
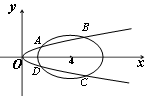
 如图,曲线M:y2=x与曲线N:(x-4)2+2y2=m2(m>0)相交于A、B、C、D四个点.
如图,曲线M:y2=x与曲线N:(x-4)2+2y2=m2(m>0)相交于A、B、C、D四个点.分析 (1)联立曲线$\left\{\begin{array}{l}{{y}^{2}=x}\\{(x-4)^{2}+2{y}^{2}={m}^{2}}\end{array}\right.$,得x2-6x+16-m2=0,由此利用根的判别式、韦达定理能求出m的取值范围.
(2)设A(x1,y1),B(x2,y2),x2>x1,y1>0,y2>0,则SABCD=(y1+y2)(x2-x1)=($\sqrt{{x}_{1}}+\sqrt{{x}_{2}}$)(x2-x1)=$\sqrt{6+2\sqrt{16-{m}^{2}}}$•$\sqrt{36-4×(16-{m}^{2})}$,令t=$\sqrt{16-{m}^{2}}$,则tSABCD=2$\sqrt{2}$$\sqrt{-{t}^{3}-3{t}^{2}+9t+27}$,设f(t)=-t3-3t2+9t+27,由导数性质能求出SABCD的最大值为16.由此能求出结果.
解答 解:(1)联立曲线$\left\{\begin{array}{l}{{y}^{2}=x}\\{(x-4)^{2}+2{y}^{2}={m}^{2}}\end{array}\right.$,消去y,得(x-4)2+2x-m2=0,
整理,得:x2-6x+16-m2=0,
根据已知条件,得$\left\{\begin{array}{l}{△=36-4(16-{m}^{2})>0}\\{{x}_{1}+{x}_{2}=6>0}\\{{x}_{1}{x}_{2}=16-{{m}^{2}>0}_{\;}}\end{array}\right.$,
解得$\sqrt{7}<m<4$.(4分)
(2)设A(x1,y1),B(x2,y2),x2>x1,y1>0,y2>0,
则SABCD=(y1+y2)(x2-x1)=($\sqrt{{x}_{1}}+\sqrt{{x}_{2}}$)(x2-x1)
=$\sqrt{{x}_{1}+{x}_{2}+2\sqrt{{x}_{1}{x}_{2}}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{6+2\sqrt{16-{m}^{2}}}$•$\sqrt{36-4×(16-{m}^{2})}$.(6分)
令t=$\sqrt{16-{m}^{2}}$,则t∈(0,3),SABCD=$\sqrt{6+2t}•\sqrt{36-4{t}^{2}}$=2$\sqrt{2}$$\sqrt{-{t}^{3}-3{t}^{2}+9t+27}$,(7分)
设f(t)=-t3-3t2+9t+27,
则令f′(t)=-3t2-6t+9=-3(t2+2t-3)=-3(t-1)(t+3)=0,
可得当t∈(0,3)时,f(x)的最大值为f(1)=32,从而SABCD的最大值为16.
此时t=1,即$\sqrt{16-{m}^{2}}$=1,则m2=15.(9分)
联立曲线M,N的方程消去y并整理得
x2-6x+1=0,解得${x}_{1}=3-2\sqrt{2}$,${x}_{2}=3+2\sqrt{2}$,
∴A点坐标为(3-2$\sqrt{2}$,$\sqrt{2}-1$),C点坐标为(3+2$\sqrt{2}$,-$\sqrt{2}-1$),
kAC=$\frac{(-\sqrt{2}-1)-(\sqrt{2}-1)}{(3+2\sqrt{2})-(3-2\sqrt{2})}$=-$\frac{1}{2}$,
则直线AC的方程为y-($\sqrt{2}-1$)=-$\frac{1}{2}$[x-(3-2$\sqrt{2}$)],(11分)
当y=0时,x=1,由对称性可知AC与BD的交点在x轴上,
即对角线AC与BD交点坐标为(1,0).(12分)
点评 本题考查实数的取值范围的求法,考查四边形的面积的最大值及此时对角线的交点坐标的求法,综合性强,难度大,对数学思维能力的要求较高.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不充分也不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b=$\frac{1}{2}$且f(a)>f($\frac{1}{a}$) | B. | b=-$\frac{1}{2}$且f(a)<f($\frac{1}{a}$) | ||
| C. | b=$\frac{1}{2}$且f(a+$\frac{1}{a}$)>f($\frac{1}{b}$) | D. | b=-$\frac{1}{2}$且f(a+$\frac{1}{a}$)<f($\frac{1}{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com