练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f（x）=ax+
    x
    x-1
    （x＞1），若a是从0，1，2三数中任取一个，b是从1，2，3，4四数中任取一个，那么f（x）＞b恒成立的概率为（　　）
    A、
    2
    3
    B、
    7
    20
    C、
    2
    5
    D、
    1
    2
    考点：古典概型及其概率计算公式
    专题：概率与统计
    分析：由恒成立和分类讨论可得当a＞0时有7种情况，当a=0时有1种情况，而总的共12种，由概率公式可得．
    解答： 解析：当a＞0时，由x＞1知f（x）=ax+
    x
    x-1

    =a（x-1）+
    1
    x-1
    +a+1≥2
    		a
    +a+1=（
    		a
    +1）2，
    ∵f（x）＞b恒成立，∵（
    		a
    +1）2＞b恒成立，
    若b=1，则a=1，2；若b=2，则a=1，2；
    若b=3，则a=1，2；若b=4，则a=2，共7种情况．
    当a=0时，f（x）=
    1
    x-1
    +1＞1，b=1适合，
    故所求概率为P=
    8
    3×4
    =
    2
    3
    ．
    故选：A
    点评：本题考查古典概型，涉及恒成立和分类讨论以及基本不等式，属中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在研究关于曲线C：
    x4
    16
    -y2=1的性质过程中，有同学得到了如下结论①曲线C关于原点、x，y轴对称 ②曲线C的渐近线为y=±
    x
    2
     ③曲线C的两个顶点分别为（-2，0），（2，0）④曲线C上的点到原点的最近距离为2．上述判断正确的编号为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A（-5，0），B（5，0），直线AM，BM相交于点M，且它们的斜率之积为-
    4
    9
    ，若设点M（x，y），则点M的轨迹方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a3+b3=9，a5+b2=11．
    （Ⅰ）求{an}，{bn}的通项公式；
    （Ⅱ）求数列{
    an
    bn
    }的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

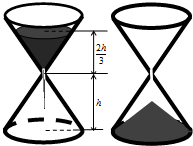    沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时．如图，某沙漏由上下两个圆锥组成，圆锥的底面直径和高均为8cm，细沙全部在上部时，其高度为圆锥高度的
    2
    3
    （细管长度忽略不计）．
    （1）如果该沙漏每秒钟漏下0.02cm3的沙，则该沙漏的一个沙时为多少秒（精确到1秒）？
    （2）细沙全部漏入下部后，恰好堆成个一盖住沙漏底部的圆锥形沙堆，求此锥形沙堆的高度（精确到0.1cm）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    高一军训时，某同学射击一次，命中10环，9环，8环的概率分别为0.13，0.28，0.31．
    （1）求射击一次，命中10环或9环的概率；
    （2）求射击一次，至少命中8环的概率；
    （3）求射击一次，命中环数小于9环的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题：
    ①函数y=sin（
    3
    2
    π+x）是偶函数；
    ②函数y=cos（2x+
    π
    4
    ）图象的一条对称轴方程为x=
    π
    8
    ；
    ③对于任意实数x，有f（-x）=-f（x），g（-x）=g（x），且x＞0时，f'（x）＞0，g'（x）＞0则x＜0时，f'（x）＞g'（x）；④函数f（2-x）与函数f（x-2）的图象关于直线x=2对称；⑤若x＞0，且x≠1则1gx+
    1
    lgx
    ≥2；
    其中真命题的序号为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=
    a
    •
    b
    ，其中向量
    a
    =（2cosx，1），
    b
    =（cosx，sin2x），x∈R．
    （1）求函数f（x）的解析式，并写出其最小正周期；
    （2）在给出的坐标系中利用五点法画出y=f（x）在区间[0，π]上的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求满足2x（2sinx-
    		3
    ）≥0，x∈（0，2π）的角α的集合（　　）
    A、（0，
    π
    3
    ）
    B、[
    π
    3
    ，
    2π
    3
    ]
    C、[
    π
    3
    ，
    π
    2
    ]
    D、[
    π
    2
    ，
    2π
    3
    ]

    查看答案和解析>>

    同步练习册答案