
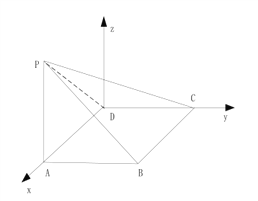
【题目】如图所示,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 是正方形,且
是正方形,且![]() ,
, ![]() .
.
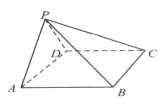
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)利用面面垂直的性质定理可得![]() 平面
平面![]() .据此有
.据此有![]() ,结合
,结合![]() 可得
可得![]() 平面
平面![]() .最后利用面面垂直的判定定理可得平面
.最后利用面面垂直的判定定理可得平面![]() 平面
平面![]() .
.
(Ⅱ)取![]() 的中点为
的中点为![]() ,
, ![]() 的中点为
的中点为![]() ,连接
,连接![]() ,以
,以![]() 的方向分别为
的方向分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系,据此可得平面
轴的正方向建立空间直角坐标系,据此可得平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,据此计算可得二面角
,据此计算可得二面角![]() 的余弦值为
的余弦值为![]() .
.
法2:若以![]() 为原点,建立空间直角坐标,则面
为原点,建立空间直角坐标,则面![]() 的法向量
的法向量![]() 面
面![]() 的法向量
的法向量![]() ,计算可得
,计算可得![]() 为钝角,则余弦值为
为钝角,则余弦值为![]() .
.
试题解析:
(Ⅰ)证明:∵底面![]() 为正方形,∴
为正方形,∴![]() .
.
又∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(Ⅱ)取![]() 的中点为
的中点为![]() ,
, ![]() 的中点为
的中点为![]() ,连接
,连接![]()
易得![]() 底面
底面![]() ,
, ![]()
以![]() 为原点,以
为原点,以![]() 的方向分别为
的方向分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系,如图,不妨设正方形的边长为2,可得
轴的正方向建立空间直角坐标系,如图,不妨设正方形的边长为2,可得![]() ,
, ![]() ,
, ![]() ,
, ![]()
设平面![]() 的一个法向量为
的一个法向量为![]()
而![]() ,
, ![]()
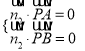 即
即![]()
取![]() 得
得![]()
设平面![]() 的一个法向量为
的一个法向量为![]()
而![]() ,
, ![]()
则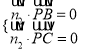 即
即![]() 取
取![]() 得
得![]()
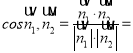
![]()
由图知所求二面角为钝角
故二面角![]() 的余弦值为
的余弦值为![]() .
.
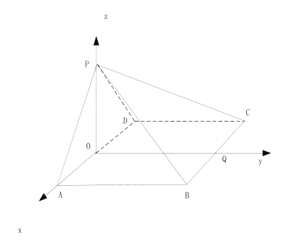
法2:若以![]() 为原点,建立空间直角坐标,如图,
为原点,建立空间直角坐标,如图,
不妨设正方形的边长为2
可得面![]() 的法向量
的法向量![]()
面![]() 的法向量
的法向量![]()
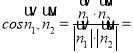
![]()
由图可得![]() 为钝角
为钝角
∴余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点
(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设不过原点O且斜率为![]() 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点
的焦点![]() 的坐标为
的坐标为![]() ,
, ![]() 的坐标为
的坐标为![]() ,且经过点
,且经过点![]() ,
, ![]() 轴.
轴.
(1)求椭圆![]() 的方程;
的方程;
(2)设过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两不同点,在椭圆
两不同点,在椭圆![]() 上是否存在一点
上是否存在一点![]() ,使四边形
,使四边形![]() 为平行四边形?若存在,求出直线
为平行四边形?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市教育局对该市普通高中学生进行学业水平测试,试卷满分120分,现从全市学生中随机抽查了10名学生的成绩,其茎叶图如下图所示:

(1)已知10名学生的平均成绩为88,计算其中位数和方差;
(2)已知全市学生学习成绩分布服从正态分布![]() ,某校实验班学生30人.
,某校实验班学生30人.
①依据(1)的结果,试估计该班学业水平测试成绩在![]() 的学生人数(结果四舍五入取整数);
的学生人数(结果四舍五入取整数);
②为参加学校举行的数学知识竞赛,该班决定推荐成绩在![]() 的学生参加预选赛若每个学生通过预选赛的概率为
的学生参加预选赛若每个学生通过预选赛的概率为![]() ,用随机变量
,用随机变量![]() 表示通过预选赛的人数,求
表示通过预选赛的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
正态分布参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在小明的婚礼上,为了活跃气氛,主持人邀请10位客人做一个游戏.第一轮游戏中,主持人将标有数字1,2,…,10的十张相同的卡片放入一个不透明箱子中,让客人依次去摸,摸到数字6,7,…,10的客人留下,其余的淘汰,第二轮放入1,2,…,5五张卡片,让留下的客人依次去摸,摸到数字3,4,5的客人留下,第三轮放入1,2,3三张卡片,让留下的客人依次去摸,摸到数字2,3的客人留下,同样第四轮淘汰一位,最后留下的客人获得小明准备的礼物.已知客人甲参加了该游戏.
(1)求甲拿到礼物的概率;
(2)设![]() 表示甲参加游戏的轮数,求
表示甲参加游戏的轮数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为2.以极点为原点,极轴为
,半径为2.以极点为原点,极轴为![]() 的正半轴,取相同的长度单位建立平面直角坐标系,直线
的正半轴,取相同的长度单位建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为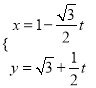 (
(![]() 为参数).
为参数).
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
, ![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,设点
,设点![]() ,在
,在![]() 中,
中, ![]() ,周长为
,周长为![]() .
.
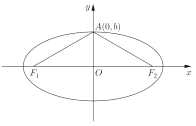
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率之和为
的斜率之和为![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(3)记第(2)问所求的定点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的一个动点,试根据
上的一个动点,试根据![]() 面积
面积![]() 的不同取值范围,讨论
的不同取值范围,讨论![]() 存在的个数,并说明理由.
存在的个数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com