
【题目】设函数![]() .
.
(1)若函数![]() 是R上的单调增函数,求实数a的取值范围;
是R上的单调增函数,求实数a的取值范围;
(2)设![]() ,
, ![]() 是
是![]() 的导函数.
的导函数.
①若对任意的![]() ,求证:存在
,求证:存在![]() 使
使![]() ;
;
②若![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() ;(2)①.证明见解析;②.证明见解析.
;(2)①.证明见解析;②.证明见解析.
【解析】试题分析:(1)由题意, ![]() 对
对![]() 恒成立,根据
恒成立,根据![]() ,等价为
,等价为![]() 对
对![]() 恒成立,即可求得
恒成立,即可求得![]() 得取值范围;(2)①分别求得
得取值范围;(2)①分别求得![]() 与
与![]() ,若
,若![]() ,则存在
,则存在![]() ,使
,使![]() ,从而得
,从而得![]() ,取
,取![]() ,则
,则![]() ,即可证明
,即可证明![]() ;②不妨设
;②不妨设![]() ,令
,令![]() ,则
,则![]() ,由(1)知函数
,由(1)知函数![]() 单调递增,则
单调递增,则![]() ,从而
,从而![]() ,根据
,根据![]() ,推出
,推出![]() ,只需证明
,只需证明![]() 成立,即只需证明
成立,即只需证明![]() 成立,设
成立,设![]() ,求得函数
,求得函数![]() 的单调性,即可证明.
的单调性,即可证明.
试题解析:(1)由题意, ![]() 对
对![]() 恒成立.
恒成立.
∵![]()
∴![]() 对
对![]() 恒成立,
恒成立,
∵![]()
∴![]() ,从而
,从而![]() .
.
(2)①![]() ,则
,则![]() .
.
若![]() ,则存在
,则存在![]() ,使
,使![]() ,不合题意.
,不合题意.
∴![]() .
.
取![]() ,则
,则![]() .
.
此时![]() .
.
∴存在![]() ,使
,使![]() .
.
②依题意,不妨设![]() ,令
,令![]() ,则
,则![]() .
.
由(1)知函数![]() 单调递增,则
单调递增,则![]() ,从而
,从而![]() .
.
∵![]()
∴![]()
∴![]() .
.
∴![]() .
.
下面证明![]() ,即证明
,即证明![]() ,只要证明
,只要证明![]() .
.
设![]() ,则
,则 在
在![]() 恒成立.
恒成立.
∴![]() 在
在![]() 单调递减,故
单调递减,故![]() ,从而
,从而![]() 得证.
得证.
∴![]() ,即
,即![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.
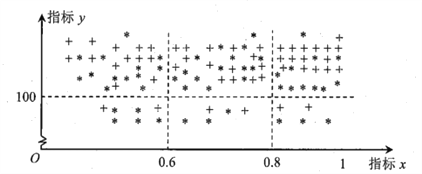
若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100~110的学生数有21人。

(Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩。
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,解答下列问题:
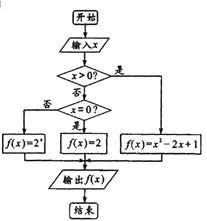
(1)求输入的![]() 的值分别为
的值分别为![]() 时,输出的
时,输出的![]() 的值;
的值;
(2)根据程序框图,写出函数![]() (
(![]() )的解析式;并求当关于
)的解析式;并求当关于![]() 的方程
的方程![]() 有三个互不相等的实数解时,实数
有三个互不相等的实数解时,实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在校体育运动会中,甲乙丙三支足球队进行单循环赛(即每两队比赛一场),共赛三场,每场比赛胜者得3分,负者得0分,没有平局.在每场比赛中,甲胜乙的概率为![]() 甲胜丙的概率为
甲胜丙的概率为![]() 乙胜丙的概率为
乙胜丙的概率为![]()
(1)求甲队获第一名且丙队获第二名的概率;
(2)求在该次比赛中甲队至少得3分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某建筑公司打算在一处工地修建一座简易储物间.该储物间室内地面呈矩形形状,面积为![]() ,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/米,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为
,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/米,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为![]() 米.
米.

(1)用![]() 表示修建储物间的总造价
表示修建储物间的总造价![]() (单位:元);
(单位:元);
(2)如何设计该储物间,可使总造价最低?最低总造价为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国Ⅱ卷)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.

(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com