
【题目】中国高铁的快速发展给群众出行带来巨大便利,极大促进了区域经济社会发展.已知某条高铁线路通车后,发车时间间隔![]() (单位:分钟)满足
(单位:分钟)满足![]() ,
,![]() ,经测算,高铁的载客量与发车时间间隔
,经测算,高铁的载客量与发车时间间隔![]() 相关:当
相关:当![]() 时高铁为满载状态,载客量为1000人;当
时高铁为满载状态,载客量为1000人;当![]() 时,载客量会在满载基础上减少,减少的人数与
时,载客量会在满载基础上减少,减少的人数与![]() 成正比,且发车时间间隔为5分钟时的载客量为100人.记发车间隔为
成正比,且发车时间间隔为5分钟时的载客量为100人.记发车间隔为![]() 分钟时,高铁载客量为
分钟时,高铁载客量为![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)若该线路发车时间间隔为![]() 分钟时的净收益
分钟时的净收益![]() (元),当发车时间间隔为多少时,单位时间的净收益
(元),当发车时间间隔为多少时,单位时间的净收益![]() 最大?
最大?
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】将一枚棋子放在一个![]() 的棋盘上,记
的棋盘上,记![]() 为从左、上数第
为从左、上数第![]() 行第
行第![]() 列的小方格,求所有的四元数组
列的小方格,求所有的四元数组![]() ,使得从
,使得从![]() 出发,经过每个小方格恰一次到达
出发,经过每个小方格恰一次到达![]() (每步为将棋子从一个小方格移到与之有共同边的另一个小方格).
(每步为将棋子从一个小方格移到与之有共同边的另一个小方格).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球运动员的投篮命中率为![]() ,他想提高自己的投篮水平,制定了一个夏季训练计划
,他想提高自己的投篮水平,制定了一个夏季训练计划![]() 为了了解训练效果,执行训练前,他统计了10场比赛的得分,计算出得分的中位数为15分,平均得分为15分,得分的方差为
为了了解训练效果,执行训练前,他统计了10场比赛的得分,计算出得分的中位数为15分,平均得分为15分,得分的方差为![]() 执行训练后也统计了10场比赛的得分,成绩茎叶图如图所示:
执行训练后也统计了10场比赛的得分,成绩茎叶图如图所示:

![]() 请计算该篮球运动员执行训练后统计的10场比赛得分的中位数、平均得分与方差;
请计算该篮球运动员执行训练后统计的10场比赛得分的中位数、平均得分与方差;
![]() 如果仅从执行训练前后统计的各10场比赛得分数据分析,你认为训练计划对该运动员的投篮水平的提高是否有帮助?为什么?
如果仅从执行训练前后统计的各10场比赛得分数据分析,你认为训练计划对该运动员的投篮水平的提高是否有帮助?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(Ⅱ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 与
与![]() 垂直的直线
垂直的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,侧面ABE⊥底面BCDE,BC=2,CD=4。
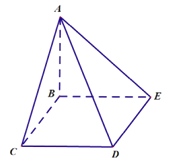
(I)证明:AB⊥面BCDE;
(II)若AD=2![]() ,求二面角C-AD-E的正弦值。
,求二面角C-AD-E的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)[选修4-4,极坐标与参数方程选讲]
在直角坐标系x0y中,曲线C1的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为p=4sin9
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为p=4sin9
(1)求曲线C1的普通方程和C2的直角坐标方程;
(Ⅱ)已知曲线C3的极坐标方程为![]() =α,(0<α<x,p∈R),点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4
=α,(0<α<x,p∈R),点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4![]() ,求实数α的值
,求实数α的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某市2011年新建住房400万m2,其中250万m2是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积比上一年增加50万m2,那么到哪一年底,
(1)该市历年所建中低价房的累计面积(以2011年为累计的第一年)将首次不少于4750万m2?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,∠BAC=120°,AC=AB=2,AA1=3.
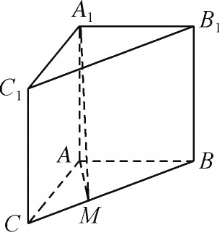
(1)求三棱柱ABC-A1B1C1的体积;
(2)若M是棱BC的一个靠近点C的三等分点,求二面角A-A1M-B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com