
【题目】在直角坐标xOy中,以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)求椭圆的直角坐标方程;
(2)已知过![]() 的直线与椭圆C交于A,B两点,且两点与左右顶点不重合,若
的直线与椭圆C交于A,B两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
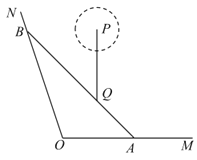
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点下的距离为10.
到其焦点下的距离为10.
(1)求抛物线C的方程;
(2)设过焦点F的的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,且抛物线在
两点,且抛物线在![]() 两点处的切线分别交x轴于
两点处的切线分别交x轴于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: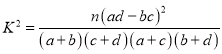 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
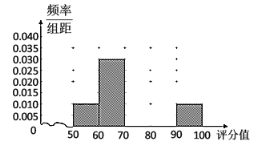
【题目】某部门在十一月份对城市居民进行了主题为空气质量问卷调查,根据每份调查表得到每个调查对象的空气质量评分值(百分制).现从收到的调查表中随机抽取20份进行统计,得到如图所示的频率分布表:
空气质量评分值 | 频数 | 频率 |
[50,60] | 2 |
|
(60.70] | 6 |
|
(70,80] |
|
|
(80,90] | 3 |
|
(90,100] | 2 |
|
(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
(2)该部门将邀请被问卷调查的部分居民参加如何提高空气质量的座谈会.在题中抽样统计的这20人中,已知空气质量评分值在区间(80,100]的5人中有2人被邀请参加座谈,求其中幸福指数评分值在区间(80,90]的仅有1人被邀请的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: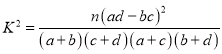 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机商家为了更好地制定手机销售策略,随机对顾客进行了一次更换手机时间间隔的调查.从更换手机的时间间隔不少于3个月且不超过24个月的顾客中选取350名作为调查对象,其中男性顾客和女性顾客的比为![]() ,商家认为一年以内(含一年)更换手机为频繁更换手机,否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人,并按性别分为两组,得到如下表所示的频数分布表:
,商家认为一年以内(含一年)更换手机为频繁更换手机,否则视为未频繁更换手机.现按照性别采用分层抽样的方法从中抽取105人,并按性别分为两组,得到如下表所示的频数分布表:
事件间隔(月) |
|
|
|
|
|
|
|
男性 | x | 8 | 9 | 18 | 12 | 8 | 4 |
女性 | y | 2 | 5 | 13 | 11 | 7 | 2 |
(1)计算表格中x,y的值;
(2)若以频率作为概率,从已抽取的105且更换手机时间间隔为3至6个月(含3个月和6个月)的顾客中,随机抽取2人,求这2人均为男性的概率;
(3)请根据频率分布表填写![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“频繁更换手机与性别有关”.
以上的把握认为“频繁更换手机与性别有关”.
频繁更换手机 | 未频繁更换手机 | 合计 | |
男性顾客 | |||
女性顾客 | |||
合计 |
附表及公式:
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
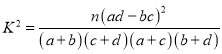
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com