
【题目】如图![]() ,
, ![]() 是圆柱的上、下底面圆的直径,
是圆柱的上、下底面圆的直径, ![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 是底面圆周上不同于
是底面圆周上不同于![]() 两点的一点,
两点的一点, ![]() .
.
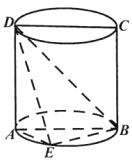
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意结合几何关系可证得![]() ,
, ![]() ,结合线面垂直的判定定理即可证得题中的结论;
,结合线面垂直的判定定理即可证得题中的结论;
(2)建立空间直角坐标系,结合平面的法向量可得二面角![]() 的余弦值是
的余弦值是![]() .
.
试题解析:
(1)由圆柱性质知: ![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() 是底面圆的直径,
是底面圆的直径, ![]() 是底面圆周上不同于
是底面圆周上不同于![]() 两点的一点,∴
两点的一点,∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解法1:过![]() 作
作![]() ,垂足为
,垂足为![]() ,由圆柱性质知平面
,由圆柱性质知平面![]() 平面
平面![]() ,
,
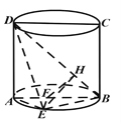
∴![]() 平面
平面![]() ,又过
,又过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
则![]() 即为所求的二面角的平面角的补角,
即为所求的二面角的平面角的补角,
![]() ,
, ![]() 易得
易得![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
由(1)知![]() ,∴
,∴![]() ,
,
∴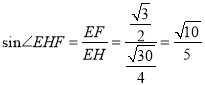 ,∴
,∴![]() ,
,
∴所求的二面角的余弦值为![]() .
.
解法2:过![]() 在平面
在平面![]() 作
作![]() ,建立如图所示的空间直角坐标系,
,建立如图所示的空间直角坐标系,
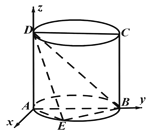
∵![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴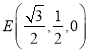 ,
, ![]() ,
, ![]() ,
,
∴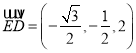 ,
, ![]() ,
,
平面![]() 的法向量为
的法向量为![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
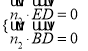 ,即
,即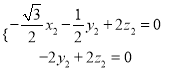 ,取
,取![]() ,
,
∴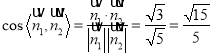 ,
,
∴所求的二面角的余弦值为![]() .
.
解法3:如图,以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴,
轴, ![]() 轴,圆柱过点
轴,圆柱过点![]() 的母线为
的母线为![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则
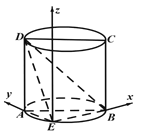
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则![]() ,
, ![]() ,即
,即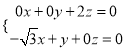 ,令
,令![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则![]() ,
, ![]() ,即
,即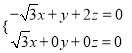 ,令
,令![]() ,则
,则![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
,
∴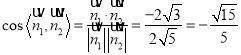 ,
,
∴所求的二面角的余弦值为![]() .
.
解法4:由(1)知可建立如图所示的空间直角坐标系:
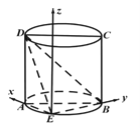
∵![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
∴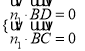 ,
,  ,
,
即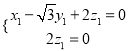 ,
, ![]() ,
,
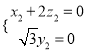 ,取
,取![]() ,
,
∴ .
.
∴所求的二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】给出下列函数:①y=x2+1;②y=﹣|x|;③y=( ![]() )x;④y=log2x;
)x;④y=log2x;
其中同时满足下列两个条件的函数的个数是( )
条件一:定义在R上的偶函数;
条件二:对任意x1 , x2∈(0,+∞),(x1≠x2),有 ![]() <0.
<0.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() ,
,![]() 称为相应于点
称为相应于点![]() 的残差(也叫随机误差));
的残差(也叫随机误差));
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.4,0.6.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入-成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣1,1),对任意x,y∈(﹣1,1),有f(x)+f(y)=f( ![]() ).且当x<0时,f(x)>0.
).且当x<0时,f(x)>0.
(1)验证函数f(x)=lg ![]() 是否满足这些条件;
是否满足这些条件;
(2)若f( ![]() )=1,f(
)=1,f( ![]() )=2,且|a|<1,|b|<1,求f(a),f(b)的值.
)=2,且|a|<1,|b|<1,求f(a),f(b)的值.
(3)若f(﹣ ![]() )=1,试解关于x的方程f(x)=﹣
)=1,试解关于x的方程f(x)=﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如表统计数据表:
收入x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据如表可得回归直线方程y= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户收入为20万元家庭年支出为( )
,据此估计,该社区一户收入为20万元家庭年支出为( )
A.11.4万元
B.11.8万元
C.15.2万元
D.15.6万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,﹣4),且倾斜角为 ![]() ,圆C的极坐标方程为ρ=4cosθ.
,圆C的极坐标方程为ρ=4cosθ.
(1)求直线l的参数方程和圆C的直角坐标方程;
(2)若直线l和圆C相交于A、B两点,求|PA||PB|及弦长|AB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com