
ЁОЬтФПЁПЩшМЏКЯ![]() ЁЂ
ЁЂ![]() ОљЮЊЪЕЪ§МЏ
ОљЮЊЪЕЪ§МЏ![]() ЕФзгМЏЃЌМЧЃК
ЕФзгМЏЃЌМЧЃК![]() ЃЛ
ЃЛ
ЃЈ1ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЪдгУСаОйЗЈБэЪО
ЃЌЪдгУСаОйЗЈБэЪО![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЕБ
ЃЌЕБ![]() ЃЌЧв
ЃЌЧв![]() ЪБЃЌЧњЯп
ЪБЃЌЧњЯп![]() ЕФНЙОрЮЊ
ЕФНЙОрЮЊ![]() ЃЌШчЙћ
ЃЌШчЙћ![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() жаЕФЫљгадЊЫижЎКЭЮЊ
жаЕФЫљгадЊЫижЎКЭЮЊ![]() ЃЌЖдгкТњзу
ЃЌЖдгкТњзу![]() ЃЌЧв
ЃЌЧв![]() ЕФШЮвте§ећЪ§
ЕФШЮвте§ећЪ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌВЛЕШЪН
ЃЌВЛЕШЪН![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШєећЪ§МЏКЯ![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЮЊЁАздЩњМЏЁБЃЌШєШЮвтвЛИіе§ећЪ§ОљЮЊећЪ§МЏКЯ
ЮЊЁАздЩњМЏЁБЃЌШєШЮвтвЛИіе§ећЪ§ОљЮЊећЪ§МЏКЯ![]() ЕФФГИіЗЧПегаЯозгМЏжаЫљгадЊЫиЕФКЭЃЌдђГЦ
ЕФФГИіЗЧПегаЯозгМЏжаЫљгадЊЫиЕФКЭЃЌдђГЦ![]() ЮЊЁА
ЮЊЁА![]() ЕФЛљЕзМЏЁБЃЌЮЪЃКЪЧЗёДцдквЛИіећЪ§МЏКЯМШЪЧздЩњМЏгжЪЧ
ЕФЛљЕзМЏЁБЃЌЮЪЃКЪЧЗёДцдквЛИіећЪ§МЏКЯМШЪЧздЩњМЏгжЪЧ![]() ЕФЛљЕзМЏЃПЧыЫЕУїРэгЩЃЎ
ЕФЛљЕзМЏЃПЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() ЃЈ3ЃЉДцдкЃЌРэгЩМћНтЮі
ЃЈ3ЃЉДцдкЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнаТЖЈвх![]() ЃЌНсКЯвбжЊжаЕФМЏКЯ
ЃЌНсКЯвбжЊжаЕФМЏКЯ![]() ЁЂ
ЁЂ![]() ЃЌПЩЕУД№АИЃЛ
ЃЌПЩЕУД№АИЃЛ
ЃЈ2ЃЉЧњЯп![]() БэЪОЫЋЧњЯпЃЌНјЖјПЩЕУ
БэЪОЫЋЧњЯпЃЌНјЖјПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]()
![]() ЃЌНсКЯ
ЃЌНсКЯ![]() Чв
Чв![]() МАЛљБОВЛЕШЪНЃЌПЩЕУ
МАЛљБОВЛЕШЪНЃЌПЩЕУ![]() НјЖјЕУЕНД№АИЃЛ
НјЖјЕУЕНД№АИЃЛ
ЃЈ3ЃЉЩшећЪ§МЏКЯ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЮЊьГВЈФЧЦѕЪ§СаЃЌМД
ЮЊьГВЈФЧЦѕЪ§СаЃЌМД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЂйгЩ![]() ЕУЃК
ЕУЃК![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЪЧздЩњМЏЃЛ
ЪЧздЩњМЏЃЛ
ЂкЖдгкШЮвт![]() ЃЌЖдгкШЮвЛе§ећЪ§
ЃЌЖдгкШЮвЛе§ећЪ§![]() ЃЌДцдкМЏКЯ
ЃЌДцдкМЏКЯ![]() ЕФвЛИігаЯозгМЏ
ЕФвЛИігаЯозгМЏ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЃЈ
ЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдйгУЪ§бЇЙщФЩЗЈжЄУїМЏКЯ
ЃЉЃЌдйгУЪ§бЇЙщФЩЗЈжЄУїМЏКЯ![]() гжЪЧ
гжЪЧ![]() ЕФЛљЕзМЏЃЎ
ЕФЛљЕзМЏЃЎ
НтЃКЃЈ1ЃЉЁп![]() ЃЛ
ЃЛ
ЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧњЯп![]() ЃЌМД
ЃЌМД![]() ЃЌдк
ЃЌдк![]() ЪББэЪОЫЋЧњЯпЃЌ
ЪББэЪОЫЋЧњЯпЃЌ
ЙЪ ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() жаЕФЫљгадЊЫижЎКЭЮЊ
жаЕФЫљгадЊЫижЎКЭЮЊ![]()
![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
Ёр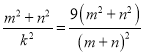
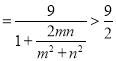 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МДЪЕЪ§![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдквЛИіећЪ§МЏКЯМШЪЧздЩњМЏгжЪЧ![]() ЕФЛљЕзМЏЃЌРэгЩШчЯТЃК
ЕФЛљЕзМЏЃЌРэгЩШчЯТЃК
ЩшећЪ§МЏКЯ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЮЊьГВЈФЧЦѕЪ§СаЃЌ
ЮЊьГВЈФЧЦѕЪ§СаЃЌ
МД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЯТжЄЃКећЪ§МЏКЯ![]() МШЪЧздЩњМЏгжЪЧ
МШЪЧздЩњМЏгжЪЧ![]() ЕФЛљЕзМЏЃЌ
ЕФЛљЕзМЏЃЌ
ЂйгЩ![]() ЕУЃК
ЕУЃК![]() ЃЌ
ЃЌ
ЙЪ![]() ЪЧздЩњМЏЃЛ
ЪЧздЩњМЏЃЛ
ЂкЖдгкШЮвт![]() ЃЌЖдгкШЮвЛе§ећЪ§
ЃЌЖдгкШЮвЛе§ећЪ§![]() ЃЌДцдкМЏКЯ
ЃЌДцдкМЏКЯ![]() ЕФвЛИігаЯозгМЏ
ЕФвЛИігаЯозгМЏ![]() ЃЌ
ЃЌ
ЪЙЕУ![]() ЃЌЃЈ
ЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЕБ![]() ЪБЃЌгЩ
ЪБЃЌгЩ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжЊНсТлГЩСЂЃЛ
ЃЌжЊНсТлГЩСЂЃЛ
МйЩшНсТлЖд![]() ЪБГЩСЂЃЌ
ЪБГЩСЂЃЌ
дђ![]() ЪБЃЌжЛаыЖдШЮКЮећЪ§
ЪБЃЌжЛаыЖдШЮКЮећЪ§![]() ЬжТлЃЌ
ЬжТлЃЌ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЙЪ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩЙщФЩМйЩшЃЌ![]() ПЩвдБэЪОЮЊМЏКЯ
ПЩвдБэЪОЮЊМЏКЯ![]() жагаЯоИіОјЖджЕаЁгк
жагаЯоИіОјЖджЕаЁгк![]() ЕФдЊЫиЕФКЭЃЎ
ЕФдЊЫиЕФКЭЃЎ
вђЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() ПЩвдБэЪОЮЊМЏКЯ
ПЩвдБэЪОЮЊМЏКЯ![]() жагаЯоИіОјЖджЕаЁгк
жагаЯоИіОјЖджЕаЁгк![]() ЕФдЊЫиЕФКЭЃЎ
ЕФдЊЫиЕФКЭЃЎ
Шє![]() ЃЌдђНсТлЯдШЛГЩСЂЃЎ
ЃЌдђНсТлЯдШЛГЩСЂЃЎ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩЙщФЩМйЩшжЊЃЌ![]() ПЩвдБэЪОЮЊМЏКЯ
ПЩвдБэЪОЮЊМЏКЯ![]() жагаЯоИіОјЖджЕаЁгк
жагаЯоИіОјЖджЕаЁгк![]() ЕФдЊЫиЕФКЭЃЎ
ЕФдЊЫиЕФКЭЃЎ
ЫљвдЃЌЕБ![]() ЪБНсТлвВГЩСЂЃЛ
ЪБНсТлвВГЩСЂЃЛ
гЩгкьГВЈФЧЦѕЪ§СаЪЧЮоНчЕФЃЌ
ЫљвдЃЌШЮвЛИіе§ећЪ§ЖМПЩвдБэЪОГЩМЏКЯ![]() ЕФвЛИігаЯозгМЏжаЫљгадЊЫиЕФКЭЃЎ
ЕФвЛИігаЯозгМЏжаЫљгадЊЫиЕФКЭЃЎ
вђДЫМЏКЯ![]() гжЪЧ
гжЪЧ![]() ЕФЛљЕзМЏЃЎ
ЕФЛљЕзМЏЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,аЈаЮМИКЮЬх![]() гЩвЛИіШ§РтжљНиШЅВПЗжКѓЫљЕУ,ЕзУц
гЩвЛИіШ§РтжљНиШЅВПЗжКѓЫљЕУ,ЕзУц![]() ВрУц
ВрУц![]() ,
,![]() ,аЈУц
,аЈУц![]() ЪЧБпГЄЮЊ2ЕФе§Ш§НЧаЮ,Еу
ЪЧБпГЄЮЊ2ЕФе§Ш§НЧаЮ,Еу![]() дкВрУц
дкВрУц![]() ЕФЩфгАЪЧОиаЮ
ЕФЩфгАЪЧОиаЮ![]() ЕФжааФ
ЕФжааФ![]() ,Еу
,Еу![]() дк
дк![]() ЩЯ,Чв
ЩЯ,Чв![]()
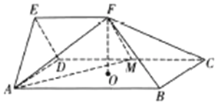
ЃЈ1ЃЉжЄУїЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓаЈУц![]() гыВрУц
гыВрУц![]() ЫљГЩЖўУцНЧЕФгрЯвжЕ.
ЫљГЩЖўУцНЧЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
ЃЈ1ЃЉЕБ![]() ЪБЃЌжЄУїЃК
ЪБЃЌжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() дк
дк![]() ЩЯгаЧвжЛгавЛИіСуЕуЃЌЧѓ
ЩЯгаЧвжЛгавЛИіСуЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙ§ЭждВ![]() ЃК
ЃК ![]() ЕФзѓгвНЙЕу
ЕФзѓгвНЙЕу![]() ЗжБ№зїжБЯп
ЗжБ№зїжБЯп![]() ЃЌ
ЃЌ ![]() НЛЭждВгк
НЛЭждВгк![]() гы
гы![]() ЃЌЧв
ЃЌЧв![]() .
.
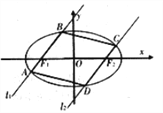
ЃЈ1ЃЉЧѓжЄЃКЕБжБЯп![]() ЕФаБТЪ
ЕФаБТЪ![]() гыжБЯп
гыжБЯп![]() ЕФаБТЪ
ЕФаБТЪ![]() ЖМДцдкЪБЃЌ
ЖМДцдкЪБЃЌ ![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
ЃЈ2ЃЉЧѓЫФБпаЮ![]() УцЛ§ЕФзюДѓжЕ.
УцЛ§ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиМЦЛЎдквЛДІКЃЬВНЈдьвЛИібјжГГЁ.
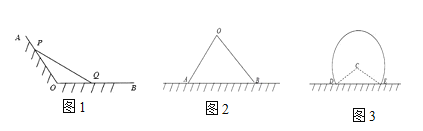
ЃЈ1ЃЉШчЭМ1ЃЌЩфЯпOAЃЌOBЮЊКЃАЖЯпЃЌ![]() ЃЌЯжгУГЄЖШЮЊ1ЧЇУзЕФЮЇЭјPQвРЭаКЃАЖЯпЮЇГЩвЛИі
ЃЌЯжгУГЄЖШЮЊ1ЧЇУзЕФЮЇЭјPQвРЭаКЃАЖЯпЮЇГЩвЛИі![]() ЕФбјжГГЁЃЌЮЪШчКЮбЁШЁЕуPЃЌQЃЌВХФмЪЙбјжГГЁ
ЕФбјжГГЁЃЌЮЪШчКЮбЁШЁЕуPЃЌQЃЌВХФмЪЙбјжГГЁ![]() ЕФУцЛ§зюДѓЃЌВЂЧѓЦфзюДѓУцЛ§.
ЕФУцЛ§зюДѓЃЌВЂЧѓЦфзюДѓУцЛ§.
ЃЈ2ЃЉШчЭМ2ЃЌжБЯпlЮЊКЃАЖЯпЃЌЯжгУГЄЖШЮЊ1ЧЇУзЕФЮЇЭјвРЭаКЃАЖЯпЮЇГЩвЛИібјжГГЁ.ЗНАИвЛЃКЮЇГЩШ§НЧаЮOABЃЈЕуAЃЌBдкжБЯпlЩЯЃЉЃЌЪЙШ§НЧаЮOABУцЛ§зюДѓЃЌЩшЦфЮЊ![]() ЃЛЗНАИЖўЃКЮЇГЩЙаЮCDEЃЈЕуDЃЌEдкжБЯпlЩЯЃЌCЪЧгХЛЁЫљдкдВЕФдВаФЧв
ЃЛЗНАИЖўЃКЮЇГЩЙаЮCDEЃЈЕуDЃЌEдкжБЯпlЩЯЃЌCЪЧгХЛЁЫљдкдВЕФдВаФЧв![]() ЃЉЃЌЦфУцЛ§ЮЊ
ЃЉЃЌЦфУцЛ§ЮЊ![]() ЃЛЪдЧѓГі
ЃЛЪдЧѓГі![]() ЕФзюДѓжЕКЭ
ЕФзюДѓжЕКЭ![]() ЃЈОљОЋШЗЕН0.01ЦНЗНЧЇУзЃЉЃЌВЂжИГіФФвЛжжЩшМЦЗНАИИќКУ.
ЃЈОљОЋШЗЕН0.01ЦНЗНЧЇУзЃЉЃЌВЂжИГіФФвЛжжЩшМЦЗНАИИќКУ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧЦцКЏЪ§
ЪЧЦцКЏЪ§![]() ЕФЕМКЏЪ§ЃЌ
ЕФЕМКЏЪ§ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђЪЙЕУ
ЃЌдђЪЙЕУ![]() ГЩСЂЕФ
ГЩСЂЕФ![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЙФРјжАдБЙЄзїШШЧщЃЌФГЙЋЫОЖдУПЮЛжАдБвЛФъРДЕФЙЄзївЕМЈАДдТНјааПМЦРДђЗжЃЛФъжеАДеежАдБЕФдТЦНОљжЕЦРбЁЙЋЫОзюМбжАдБВЂИјгшЯргІНБРј.вбжЊжАдБ![]() вЛФъРДЕФЙЄзївЕМЈЗжЪ§ЕФОЅвЖЭМШчЭМЫљЪОЃК
вЛФъРДЕФЙЄзївЕМЈЗжЪ§ЕФОЅвЖЭМШчЭМЫљЪОЃК
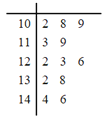
ЃЈ1ЃЉИљОнжАдБ![]() ЕФвЕМЈОЅвЖЭМЧѓГіЫћетвЛФъЕФЙЄзївЕМЈЕФжаЮЛЪ§КЭЦНОљЪ§ЃЛ
ЕФвЕМЈОЅвЖЭМЧѓГіЫћетвЛФъЕФЙЄзївЕМЈЕФжаЮЛЪ§КЭЦНОљЪ§ЃЛ
ЃЈ2ЃЉШєМЧжАдБ![]() ЕФЙЄзївЕМЈЕФдТЦНОљЪ§ЮЊ
ЕФЙЄзївЕМЈЕФдТЦНОљЪ§ЮЊ![]() .
.
ЂйвбжЊИУЙЋЫОЛЙга6ЮЛжАдБЕФвЕМЈдк100вдЩЯЃЌЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдкет6ШЫЕФвЕМЈРяЫцЛњГщШЁ2ИіЪ§ОнЃЌЧѓЧЁга1ИіЪ§ОнТњзу
ЃЌдкет6ШЫЕФвЕМЈРяЫцЛњГщШЁ2ИіЪ§ОнЃЌЧѓЧЁга1ИіЪ§ОнТњзу![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЕФИХТЪЃЛ
ЃЉЕФИХТЪЃЛ
ЂкгЩгкжАдБ![]() ЕФвЕМЈИпЃЌБЛЙЋЫОЦРЮЊФъЖШзюМбжАдБЃЌдкЙЋЫОФъЛсЩЯЭЈЙ§ГщНБаЮЪНСьШЁНБН№.ЙЋЫОзМБИСЫ9еХПЈЦЌЃЌЦфжага1еХПЈЦЌЩЯБъзЂНБН№ЮЊ6ЧЇдЊЃЌ4еХПЈЦЌЕФНБН№ЮЊ4ЧЇдЊЃЌСэЭт4еХЕФНБН№ЮЊ2ЧЇдЊ.ЙцдђЪЧЃКЛёНБжАдБашвЊДг9еХПЈЦЌжаЫцЛњГщГі3еХЃЌет3еХПЈЦЌЩЯЕФН№ЖюЪ§жЎКЭОЭЪЧИУжАдБЫљЕУНБН№.МЧжАдБ
ЕФвЕМЈИпЃЌБЛЙЋЫОЦРЮЊФъЖШзюМбжАдБЃЌдкЙЋЫОФъЛсЩЯЭЈЙ§ГщНБаЮЪНСьШЁНБН№.ЙЋЫОзМБИСЫ9еХПЈЦЌЃЌЦфжага1еХПЈЦЌЩЯБъзЂНБН№ЮЊ6ЧЇдЊЃЌ4еХПЈЦЌЕФНБН№ЮЊ4ЧЇдЊЃЌСэЭт4еХЕФНБН№ЮЊ2ЧЇдЊ.ЙцдђЪЧЃКЛёНБжАдБашвЊДг9еХПЈЦЌжаЫцЛњГщГі3еХЃЌет3еХПЈЦЌЩЯЕФН№ЖюЪ§жЎКЭОЭЪЧИУжАдБЫљЕУНБН№.МЧжАдБ![]() ЛёЕУЕФНБН№ЮЊ
ЛёЕУЕФНБН№ЮЊ![]() ЃЈЧЇдЊЃЉЃЌЧѓ
ЃЈЧЇдЊЃЉЃЌЧѓ![]() ЕФЗжВМСаКЭЦкЭћ.
ЕФЗжВМСаКЭЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
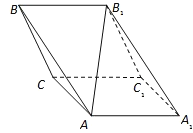
ЁОЬтФПЁПаБШ§РтжљABCЉA1B1C1ЃЌвбжЊВрУцBB1C1CгыЕзУцABCДЙжБЧвЁЯBCA=90ЁуЃЌЁЯB1BC=60ЁуЃЌBC=BB1=2ЃЌШєЖўУцНЧAЉB1BЉCЮЊ30Ёу
ЃЈ1ЃЉЧѓAB1гыЦНУцBB1C1CЫљГЩНЧЕФе§ЧажЕЃЛ
ЃЈ2ЃЉдкЦНУцAA1B1BФкеввЛЕуPЃЌЪЙШ§РтзЖPЉBB1CЮЊе§Ш§РтзЖЃЌВЂЧѓPЕНЦНУцBB1CОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
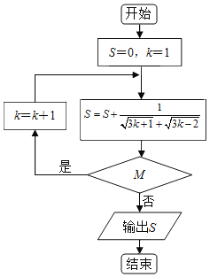
ЁОЬтФПЁПФГГЬађПђЭМШчЭМЫљЪОЃЌШєЪфГі![]() ЃЌдђХаЖЯПђжа
ЃЌдђХаЖЯПђжа![]() ЮЊЃЈ ЃЉ
ЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com