
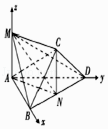
【题目】如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM= ![]()

(1)求证:DM⊥平面ABC;
(2)求二面角C﹣BM﹣D的大小.
【答案】
(1)证明:法一(几何法):如图,取BD中点N,连结AN,CN,MN,
∵将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,
∴AN⊥BD,CN⊥BD,
∵平面ABD丄平面CBD,平面ABD∩平面CBD=BD,CN平面CBD,CN⊥BD,
∴CN⊥平面ABD,又AM⊥平面ABD,∴CN∥AM,
又CN=AM=AN= ![]() ,∴AMCN是正方形,∴AC⊥MN,
,∴AMCN是正方形,∴AC⊥MN,
由BD⊥AN,BD⊥CN,AN∩CN=N,得BD⊥平面AMCN,∴BD⊥AC,
又BD∩MN=N,∴AC⊥平面BDM,∴AC⊥MD,
∵AM⊥平面ABD,∴AM⊥AB,
又AB⊥AD,AM∩AD=A,∴AB⊥平面AMD,
∴AB⊥DM,又AC⊥DM,AB∩AC=A,
∴DM⊥平面ABC.
法二(向量法):如图,取BD中点N,连结AN,CN,MN,
∵将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,
∴AN⊥BD,CN⊥BD,
∵平面ABD丄平面CBD,平面ABD∩平面CBD=BD,CN平面CBD,CN⊥BD,
∴CN⊥平面ABD,
以A为原点,AB、AD、AM所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(1,1, ![]() ),D(0,2,0),M(0,0,
),D(0,2,0),M(0,0, ![]() ),
),
![]() =(2,0,0),
=(2,0,0), ![]() =(1,1,
=(1,1, ![]() ),
), ![]() =(0,﹣2,
=(0,﹣2, ![]() ),
),
∵ ![]() =0,
=0, ![]() =0,
=0,
∴DM⊥AB,DM⊥AC,
又AB∩AC=A,∴DM⊥平面ABC
(2)解:(2)B(2,0,0),C(1,1, ![]() ),D(0,2,0),M(0,0,
),D(0,2,0),M(0,0, ![]() ),
),
∴ ![]() =(﹣2,0,
=(﹣2,0, ![]() ),
), ![]() =(﹣1,1,
=(﹣1,1, ![]() ),
), ![]() =(﹣2,2,0),
=(﹣2,2,0),
设平面CBM的法向量 ![]() =(x,y,z),
=(x,y,z),
则 ![]() ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,
=(1,﹣1, ![]() ),
),
设平面DBM的法向量 ![]() =(a,b,c),
=(a,b,c),
则 ![]() ,取a=1,得
,取a=1,得 ![]() =(1,1,
=(1,1, ![]() ),
),
∴cos< ![]() >=
>=  =
= ![]() ,
,
设二面角C﹣BM﹣D的平面角为θ,由图知θ为锐角,
∴cosθ= ![]() ,则θ=
,则θ= ![]() ,
,
∴二面角C﹣BM﹣D的大小为 ![]() .
.
【解析】(1)法一(几何法):取BD中点N,连结AN,CN,MN,推导出AN⊥BD,CN⊥BD,从而CN⊥平面ABD,再求出AM⊥平面ABD,从而CN∥AM,推导出AC⊥MN,BD⊥AC,AC⊥MD,从而AM⊥平面ABD,进而AM⊥AB,再由AB⊥AD,得AB⊥平面AMD,由此能证明DM⊥平面ABC.法二(向量法)取BD中点N,连结AN,CN,MN,以A为原点,AB、AD、AM所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能证明DM⊥平面ABC.(2)取BD中点N,连结AN,CN,MN,以A为原点,AB、AD、AM所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,求出平面CBM的法向量和平面DBM的法向量,利用向量法能求出二面角C﹣BM﹣D的大小.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,过椭圆 ![]() 右焦点的直线
右焦点的直线 ![]() 交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为
交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设另一直线l与椭圆C交于A,B两点,原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,已知O为坐标原点,点A、B的坐标分别为(1,1)、(﹣3,3).若动点P满足 ![]() ,其中λ、μ∈R,且λ+μ=1,则点P的轨迹方程为( )
,其中λ、μ∈R,且λ+μ=1,则点P的轨迹方程为( )
A.x﹣y=0
B.x+y=0
C.x+2y﹣3=0
D.(x+1)2+(y﹣2)2=5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等比数列,an>0,a3=12,且a2 , a4 , a2+36成等差数列.
(1)求数列{an}的通项公式;
(2)设{bn}是等差数列,且b3=a3 , b9=a5 , 求b3+b5+b7+…+b2n+1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( ) 
A.2017×22016
B.2018×22015
C.2017×22015
D.2018×22016
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,=0.02,则输出的结果为( ) 
A.3
B.2.5
C.2.45
D.2.4495
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣a)lnx+b.
(1)当a=0时,讨论函数f(x)在[ ![]() ,+∞)上的零点个数;
,+∞)上的零点个数;
(2)当a>1且函数f(x)在(1,e)上有极小值时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn . 已知a1=2,Sn+1=4an+2.
(1)设bn=an+1﹣2an , 证明数列{bn}是等比数列;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是菱形, ![]() ,PA=PD,F为AD的中点,PD⊥BF.
,PA=PD,F为AD的中点,PD⊥BF. 
(1)求证:AD⊥PB;
(2)若菱形ABCD的边长为6,PA=5,求四面体PBCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com