
【题目】如图,设椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,A,B分别为椭圆C的左、右顶点,F为右焦点.直线y=6x与C的交点到y轴的距离为
,A,B分别为椭圆C的左、右顶点,F为右焦点.直线y=6x与C的交点到y轴的距离为 ![]() ,过点B作x轴的垂线l,D为l 上异于点B的一点,以BD为直径作圆E.
,过点B作x轴的垂线l,D为l 上异于点B的一点,以BD为直径作圆E.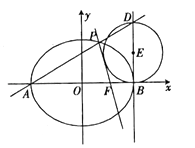
(1)求C 的方程;
(2)若直线AD与C的另一个交点为P,证明PF与圆E相切.
【答案】
(1)解:由题意可知, ![]() ,∴a=2c,
,∴a=2c,
又a2=b2+c2,则b2=3c2.
设椭圆C的方程为 ![]() ,
,
联立  ,解得x=
,解得x= ![]() ,∴c=1,a=2,b2=3.
,∴c=1,a=2,b2=3.
故椭圆C的方程为 ![]() ;
;
(2)证明:由(1)可得F(1,0),设圆E的圆心为(2,t)(t≠0),则D(2,2t),
则圆E的半径R=t.
直线AD的方程为y= ![]() .
.
联立  ,得(3+t2)x2+4t2x+4t2﹣12=0.
,得(3+t2)x2+4t2x+4t2﹣12=0.
由 ![]() ,得
,得 ![]() ,
, ![]() .
.
直线PF的方程为  ,
,
即2tx+(t2﹣1)y﹣2t=0.
∵点E(2,t)到直线PF的距离为d= ![]() ,
,
∴直线PF与圆E相切.
【解析】(1)根据题意得到![]() ,再联立直线方程,得到交点坐标,结合距离为
,再联立直线方程,得到交点坐标,结合距离为![]() ,可得到椭圆的方程,(2)由椭圆方程得出焦点F的坐标,设其圆E的圆心坐标和半径,得到直线AD的方程,联立椭圆方程得到P点的坐标,表示出PF的直线方程,根据点E到PF的距离不难得到PF与圆E相切.
,可得到椭圆的方程,(2)由椭圆方程得出焦点F的坐标,设其圆E的圆心坐标和半径,得到直线AD的方程,联立椭圆方程得到P点的坐标,表示出PF的直线方程,根据点E到PF的距离不难得到PF与圆E相切.


科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )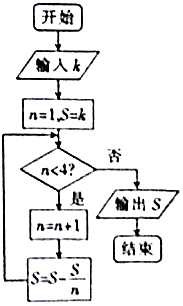
A.4.5
B.6
C.7.5
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2=r2(r>0)与直线l0:y= ![]() 相切,点A为圆C1上一动点,AN⊥x轴于点N,且动点M满足
相切,点A为圆C1上一动点,AN⊥x轴于点N,且动点M满足 ![]() ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.
(1)求动点M的轨迹曲线C的方程;
(2)若直线l与曲线C相交于不同的两点P、Q且满足以PQ为直径的圆过坐标原点O,求线段PQ长度的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等腰梯形ABCD中AB∥CD,AB=2CD=4,∠BAD=60°,双曲线以A,B为焦点,且与线段CD(包括端点C、D)有两个交点,则该双曲线的离心率的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《庄子天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )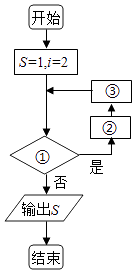
A.①i≤7?②s=s﹣ ![]() ③i=i+1
③i=i+1
B.①i≤128?②s=s﹣ ![]() ③i=2i
③i=2i
C.①i≤7?②s=s﹣ ![]() ③i=i+1
③i=i+1
D.①i≤128?②s=s﹣ ![]() ③i=2i
③i=2i
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}及{bn}中,an+1=an+bn+ ![]() =1.设
=1.设 ![]() ,则数列{cn}的前n项和为( )
,则数列{cn}的前n项和为( )
A.![]()
B.2n+2﹣4
C.3×2n+2n﹣4
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程是 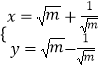 (m为参数),直线l交曲线C1于A,B两点;以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=4sin(θ﹣
(m为参数),直线l交曲线C1于A,B两点;以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=4sin(θ﹣ ![]() ),点P(ρ,
),点P(ρ, ![]() )在曲线C2上.
)在曲线C2上.
(1)求曲线C1的普通方程及点P的直角坐标;
(2)若直线l的倾斜角为 ![]() 且经过点P,求|PA|+|PB|的值.
且经过点P,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() .
.
(1)求函数 ![]() 的单调增区间;
的单调增区间;
(2)若 ![]() ,解不等式
,解不等式 ![]() ;
;
(3)若 ![]() ,且对任意
,且对任意 ![]() ,方程
,方程 ![]() 在
在 ![]() 总存在两不相等的实数根,求
总存在两不相等的实数根,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com