
【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品![]() 、
、![]() ,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表:
,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表:
产品A(件) | 产品B(件) | ||
研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
【答案】解:设搭载产品A![]() 件,产品B y件,
件,产品B y件,
 则预计收益
则预计收益![]() .
.
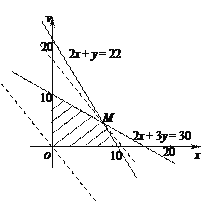
则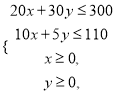 作出可行域,如图;
作出可行域,如图;
作出直线![]() 并平移.
并平移.
由图象得,当直线经过M点时, z能取得最大值,
![]() , 解得
, 解得![]() , 即
, 即![]() .
.
所以z=80×9+60×4=960(万元).
答:应搭载产品A 9件,产品B 4件,可使得利润最多达到960万元.
【解析】试题分析:设搭载A产品![]() 件,B产品
件,B产品![]() 件,依据题意得到变量x,y的线性约束条件及目标函数,然后按照线性规划求最值的步骤求解即可.但注意本题是整点问题,即一注意变量x,y的范围,二注意可行域的边界交点是否为整点.
件,依据题意得到变量x,y的线性约束条件及目标函数,然后按照线性规划求最值的步骤求解即可.但注意本题是整点问题,即一注意变量x,y的范围,二注意可行域的边界交点是否为整点.
试题解析:设搭载A产品![]() 件,B产品
件,B产品![]() 件,
件,
则总预计收益![]()
由题意知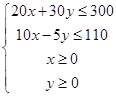 ,且
,且![]() ,
,
由此作出可行域如图所示,
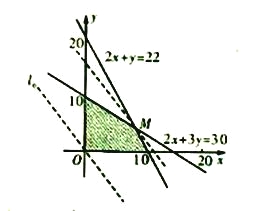
作出直线![]() 并平移,由图象知,
并平移,由图象知,
当直线经过M点时, ![]() 能取到最大值,
能取到最大值,
由![]() 解得
解得![]() 且满足
且满足![]() ,
,
即![]() 是最优解,
是最优解,
所以![]() (万元),
(万元),
答:搭载A产品9件,B产品4件,能使总预计收益达到最大值,最大预计收益为960万元.


科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD的顶点P在底面ABCD上的投影恰好是A,其正视图与侧视图都是腰长为a的等腰直角三角形.则在四棱锥P﹣ABCD的任意两个顶点的连线中,互相垂直的异面直线共有 对.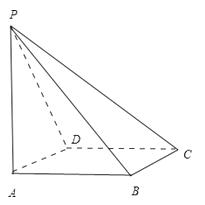
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() 是函数
是函数![]() 的极值点,1为函数
的极值点,1为函数![]() 的一个零点,求函数
的一个零点,求函数![]() 在
在![]() 上的最小值.
上的最小值.
(2)当![]() 时,函数
时,函数![]() 与
与![]() 轴在
轴在![]() 内有两个不同的交点,求
内有两个不同的交点,求![]() 的取值范围.(其中
的取值范围.(其中![]() 是自然对数的底数)
是自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,数列{an}满足a1=1,an+1=f(an)(n∈N*).
,数列{an}满足a1=1,an+1=f(an)(n∈N*).
(1)证明数列{![]() }是等差数列,并求出数列{an}的通项公式;
}是等差数列,并求出数列{an}的通项公式;
(2)记Sn=a1a2+a2a3+…+anan+1,求Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,且f(1)=2.
,且f(1)=2.
(1)求m的值;
(2)判断f(x)的奇偶性;
(3)用定义法证明f(x)在区间(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次运动会中甲、乙两名射击运动员决赛中各射击十次的成绩(环)如下:

(1)用茎叶图表示甲、乙两个人的成绩;
(2)根据茎叶图分析甲、乙两人的成绩;
(3)计算两个样本的平均数![]() 和标准差
和标准差![]() ,并根据计算结果估计哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com