
【题目】如图,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.
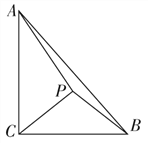
(1)若P是等腰直角三角形PBC的直角顶点,求PA的长;
(2)若∠BPC=![]() ,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
【答案】(1) ![]() (2)S(θ)=
(2)S(θ)=![]() ,S(θ)的最大值为
,S(θ)的最大值为![]()
【解析】试题分析:(1)在△PAC中,已知两边一角求第三边,根据余弦定理可得(2)先由正弦定理用θ表示PC,再根据三角形面积公式得S(θ),利用二倍角公式以及配角公式将S(θ)化为基本三角函数形式,再根据正弦函数性质求最大值
试题解析: 解 (1)解法一:∵P是等腰直角三角形PBC的直角顶点,且BC=2,
∴∠PCB=![]() ,PC=
,PC=![]() ,
,
又∵∠ACB=![]() ,∴∠ACP=
,∴∠ACP=![]() ,
,
在△PAC中,由余弦定理得PA2=AC2+PC2-2AC·PCcos![]() =5,∴PA=
=5,∴PA=![]() .
.
解法二:依题意建立如图直角坐标系,则有C(0,0),B(2,0),A(0,3),
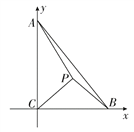 ∵△PBC是等腰直角三角形,∠ACB=
∵△PBC是等腰直角三角形,∠ACB=![]() ,
,
∴∠ACP=![]() ,∠PBC=
,∠PBC=![]() ,
,
∴直线PC的方程为y=x,直线PB的方程为y=-x+2,
由![]() 得P(1,1),
得P(1,1),
∴PA=![]() =
=![]() ,
,
(2)在△PBC中,∠BPC=![]() ,∠PCB=θ,
,∠PCB=θ,
∴∠PBC=![]() -θ,
-θ,
由正弦定理得![]() =
=![]() =
=![]() ,
,
∴PB=![]() sinθ,PC=
sinθ,PC=![]() sin
sin![]() ,
,
∴△PBC的面积S(θ)=![]() PB·PCsin
PB·PCsin![]()
=![]() sin
sin![]() sinθ
sinθ
=2sinθcosθ-![]() sin2θ=sin2θ+
sin2θ=sin2θ+![]() cos2θ-
cos2θ-![]()
=![]() sin
sin![]() -
-![]() ,θ∈
,θ∈![]() ,
,
∴当θ=![]() 时,△PBC面积的最大值为
时,△PBC面积的最大值为![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(16x+k)﹣2x (k∈R)是偶函数.
(1)求k;
(2)若不等式m﹣1≤f(x)≤2m+log217在x∈[﹣1, ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知中心在原点,焦点在x轴上的双曲线C的离心率为 ![]() ,且双曲线C与斜率为2的直线l有一个公共点P(﹣2,0).
,且双曲线C与斜率为2的直线l有一个公共点P(﹣2,0).
(1)求双曲线C的方程及它的渐近线方程;
(2)求以直线l与坐标轴的交点为焦点的抛物线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列叙述: ①若α,β均为第一象限,且α>β,则sinα>sinβ
②函数f(x)=sin(2x﹣ ![]() )在区间[0,
)在区间[0, ![]() ]上是增函数;
]上是增函数;
③函数f(x)=cos(2x+ ![]() )的一个对称中心为(﹣
)的一个对称中心为(﹣ ![]() ,0)
,0)
④记min{a,b}= ![]() ,若函数f(x)=min{sinx,cosx},则f(x)的值域为[﹣1,
,若函数f(x)=min{sinx,cosx},则f(x)的值域为[﹣1, ![]() ].
].
其是叙述正确的是(请填上序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)的右焦点为F2(1,0),点H(2,
=1(a>b>0)的右焦点为F2(1,0),点H(2, ![]() )在椭圆上.
)在椭圆上. 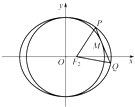
(1)求椭圆的方程;
(2)点M在圆x2+y2=b2上,且M在第一象限,过M作圆x2+y2=b2的切线交椭圆于P,Q两点,问:△PF2Q的周长是否为定值?如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数f(x)中,满足“对任意x1、x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )
A.f(x)=(x﹣1)2
B.f(x)=ex
C.f(x)= ![]()
D.f(x)=ln(x+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com