
【题目】已知函数f(x)=sin2ωx+2 ![]() cosωxsinωx+sin(ωx+
cosωxsinωx+sin(ωx+ ![]() )sin(ωx﹣
)sin(ωx﹣ ![]() )(ω>0),且f(x)的最小正周期为π.
)(ω>0),且f(x)的最小正周期为π.
(1)求ω的值;
(2)求函数f(x)在区间(0,π)上的单调增区间.
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以 ![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为 ![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):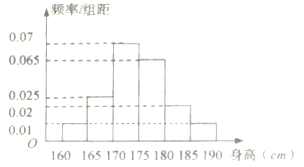
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在 ![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在 ![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上. (I)求证:BC⊥平面ACFE;
(II)当EM为何值时,AM∥平面BDF?证明你的结论.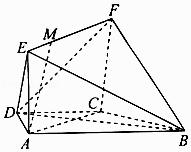
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2﹣2(a+1)x+3(a∈R).
(1)若函数f(x)在 ![]() 单调递减,求实数a的取值范围;
单调递减,求实数a的取值范围;
(2)令h(x)= ![]() ,若存在
,若存在 ![]() ,使得|h(x1)﹣h(x2)|≥
,使得|h(x1)﹣h(x2)|≥ ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若抛物线y2=2px上恒有关于直线x+y﹣1=0对称的两点A,B,则p的取值范围是( )
A.(﹣ ![]() ,0)
,0)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(|sinx|+|cosx|)﹣ ![]() sin2x﹣1,若f(
sin2x﹣1,若f( ![]() )=
)= ![]() ﹣
﹣ ![]() .
.
(1)求a的值,并写出函数f(x)的最小正周期(不需证明);
(2)是否存在正整数k,使得函数f(x)在区间[0,kπ]内恰有2017个零点?若存在,求出k的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,给出以下结论: ①直线A1B与B1C所成的角为60°;
②若M是线段AC1上的动点,则直线CM与平面BC1D所成角的正弦值的取值范围是 ![]() ;
;
③若P,Q是线段AC上的动点,且PQ=1,则四面体B1D1PQ的体积恒为 ![]() .
.
其中,正确结论的个数是( )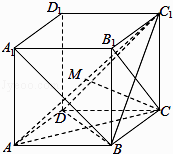
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2﹣(1+a)x+y2﹣ay+a=0(a∈R). (Ⅰ) 若a=1,求直线y=x被圆C所截得的弦长;
(Ⅱ) 若a>1,如图,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M的动直线l与圆O:x2+y2=4相交于A,B两点.问:是否存在实数a,使得对任意的直线l均有∠ANM=∠BNM?若存在,求出实数a的值,若不存在,请说明理由.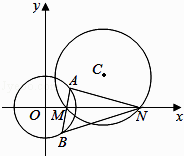
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=| ![]() ﹣ax|,若对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥m,则实数m的取值范围为( )
﹣ax|,若对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥m,则实数m的取值范围为( )
A.(﹣∞,0]
B.(﹣∞,1]
C.(﹣∞,2]
D.(﹣∞,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com