
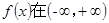 上满足以
上满足以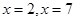 为对称轴,且在
为对称轴,且在 上只有
上只有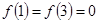 ,试求方程
,试求方程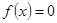 在
在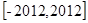 根的个数为( )
根的个数为( )| A.803个 | B.804个 | C.805个 | D.806个 |


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源:不详 题型:解答题
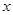 万元,每件产品的成本将降低
万元,每件产品的成本将降低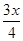 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少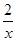 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为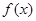 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)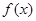 的函数解析式;
的函数解析式;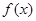 的最大值,以及
的最大值,以及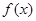 取得最大值时
取得最大值时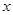 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
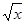 )2 ②y=x与y=
)2 ②y=x与y=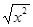 ③y=x2+1与y=t2+1 ④y=
③y=x2+1与y=t2+1 ④y=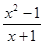 与y=x-1.表示同一函数的组数是( )
与y=x-1.表示同一函数的组数是( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com