设函数f(x)=x2+(m-1)x-2m-1(m∈R),
(1)设x1,x2为方程f(x)=0的两实根,求g(m)=x12+x22的最小值;
(2)是否存在正数a和常数m,使得x∈[0,a]时,f(x)的值域也为[0,a]?若有,求出所有a和m的值;若没有,也请说明理由.
解:(1)△=(m-1)
2+4(2m+1)≥0?m∈(-∞,-5]∪[-1,+∞)
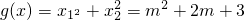
=(m+1)
2+2
故m=-1时,g(x)
min=2.
(2)假设存在正数a和常数m满足题意,则f(x)
min=0.
①若f(0)=0,则m=-

,此时f(x)=x
2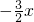
当x
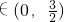
时,f(x)<0,不符题意,舍;
②若f(a)=0,则f(0)=a,a=-2m-1
所以f(a)=(-2m-1)2+(m-1)(-2m-1)-2m-1=0,
得m=-

(舍)或m=-1,a=1,经检验符合题意;
③若
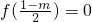
,则m
2+6m+5=0?m=-1(符合题意)或m=-5
当m=-5时,f(x)=(x-3)
2,x∈[0,a]上的值域为[0,a].
因为f(0)=9,故
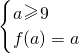
无实数解;
综上知,仅当a=1,m=-1时满足题意.
分析:(1)判断方程有两个根时m的范围,通过韦达定理得到g(m)=x
12+x
22的表达式,然后求解最小值;
(2)存在正数a和常数m,使得x∈[0,a]时,f(x)的值域也为[0,a],利用二次函数单调性,通过分类讨论求出所有a和m的值.
点评:本题考查二次函数的性质,函数的单调性的应用,分类讨论思想的应用,考查转化思想与计算能力.

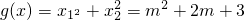 =(m+1)2+2
=(m+1)2+2 ,此时f(x)=x2
,此时f(x)=x2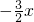
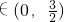 时,f(x)<0,不符题意,舍;
时,f(x)<0,不符题意,舍; (舍)或m=-1,a=1,经检验符合题意;
(舍)或m=-1,a=1,经检验符合题意;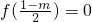 ,则m2+6m+5=0?m=-1(符合题意)或m=-5
,则m2+6m+5=0?m=-1(符合题意)或m=-5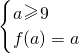 无实数解;
无实数解;
