
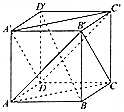
| A. | 平面ACB′∥平面A′C′D | B. | B′C⊥BD′ | ||
| C. | B′C⊥DC′ | D. | BD′⊥平面A′C′D |
分析 在A中,由AC∥A'C′,AB′∥DC′,得平面ACB′∥平面A′C′D;在B中,由B′C⊥D′C′,B′C⊥BC′,得到B′C⊥平面BD′C′,从而B′C⊥BD′;在C中,由DC′∥AB′,△AB′C是等边三角形,知B′C与DC′所成角为60°;在D中,由BD′⊥A′C′,BD′⊥A′D,知BD′⊥平面A′C′D.
解答 解:由ABCD-A′B′C′D′为正方体,知:
在A中,∵AC∥A'C′,AB′∥DC′,
且AC∩AB′=A,A′C′∩DC′=C′,
∴平面ACB′∥平面A′C′D,故A正确;
在B中,∵B′C⊥D′C′,B′C⊥BC′,
D′C′∩BC′=C′,∴B′C⊥平面BD′C′,
∵BD′?平面BD′C′,∴B′C⊥BD′,故B正确;
在C中,∵DC′∥AB′,△AB′C是等边三角形,
∴B′C与DC′所成角为60°,故C错误;
在D中,与B同理,能证明BD′⊥A′C′,BD′⊥A′D,
∴BD′⊥平面A′C′D,故D正确.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


科目:高中数学 来源: 题型:选择题
| P(K2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有95% 把握说事件A与B有关 | B. | 有95% 把握说事件A与B无关 | ||
| C. | 有99% 把握说事件A与B有关 | D. | 有99% 把握说事件A与B无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com