
【题目】给出下列命题:
①若(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a1|+|a2|+|a3|+|a4|+|a5|=32
②α,β,γ是三个不同的平面,则“γ⊥α,γ⊥β”是“α∥β”的充分条件
③已知sin![]() =
=![]() ,则cos
,则cos![]() =
=![]() .其中正确命题的个数为( )
.其中正确命题的个数为( )
A.0 B.1
C.2 D.3
【答案】B
【解析】对于①,由(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5得a1<0,a2>0,a3<0,a4>0,a5<0,
取x=-1,得a0-a1+a2-a3+a4-a5=(1+1)5=25,再取x=0得a0=(1-0)5=1,所以|a1|+|a2|+|a3|+|a4|+|a5|=-a1+a2-a3+a4-a5=31,即①不正确;
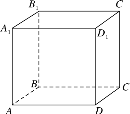
对于②,如图所示的正方体ABCD-A1B1C1D1中,平面ABB1A1⊥平面ABCD,平面ADD1A1⊥平面ABCD,但平面ABB1A1与平面ADD1A1不平行,所以②不正确;
对于③,因为sin![]() =
=![]() ,所以cos
,所以cos![]() =cos
=cos![]() =1-2sin2
=1-2sin2![]() =1-2×
=1-2×![]() 2=
2=![]() ,所以③正确.
,所以③正确.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+ax+b(a,b∈R)的定义域为[-1,1],且|f(x)|的最大值为M.
(1)证明:|1+b|≤M;
(2)证明:M≥![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当
的图象.当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】比较下列各组中两个值的大小 :
(1)ln0.3,ln2; (2)loga3.1,loga5.2(a>0,且a≠1);
(3)log30.2,log40.2; (4)log3π,logπ3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
问题解决
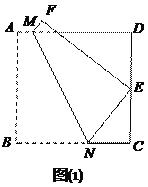
如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C、D重合),压平后得到折痕MN.当![]() 时,求
时,求![]() 的值.
的值.
类比归纳
在图(1)中,若![]() 则
则![]() 的值等于 ;若
的值等于 ;若![]() 则
则![]() 的值等于 ;若
的值等于 ;若![]() (n为整数),则
(n为整数),则![]() 的值等于 .(用含
的值等于 .(用含![]() 的式子表示)
的式子表示)
联系拓广
如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C、D重合),压平后得到折痕MN设![]() ,则
,则![]() 的值等
的值等
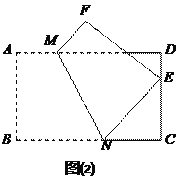
 于 ▲ .(用含
于 ▲ .(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
求数学成绩![]() 关于物理成绩
关于物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]()
若某位学生的物理成绩为80分,预测他的数学成绩;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com