
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】x,y 满足约束条件 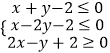 ,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
A.![]() 或﹣1
或﹣1
B.2 或 ![]()
C.2 或1
D.2 或﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数a>0,函数f(x)=ln(1+ax)﹣ ![]() .
.
(Ⅰ)讨论f(x)在区间(0,+∞)上的单调性;
(Ⅱ)若f(x)存在两个极值点x1 , x2 , 且f(x1)+f(x2)>0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数).现随机抽取20天的指数(见下表),将指数不低于8.5视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 | 7.1 | 8.3 | 7.3 | 9.5 | 8.6 | 7.7 | 8.7 | 8.8 | 8.7 | 9.1 |
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 | 7.4 | 8.5 | 9.7 | 8.4 | 9.6 | 7.6 | 9.4 | 8.9 | 8.3 | 9.3 |
(Ⅰ)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(Ⅱ)以这20天的数据估计我市总体空气质量(天数很多).若从我市总体空气质量指数中随机抽取3天的指数,用X表示抽到空气质量为优良的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有 ![]() 种取法.在这
种取法.在这 ![]() 种取法中,可以分成两类:一类是取出的m个球全部为白球,共有
种取法中,可以分成两类:一类是取出的m个球全部为白球,共有 ![]() 种取法;另一类是取出的m个球有m﹣1个白球和1个黑球,共有
种取法;另一类是取出的m个球有m﹣1个白球和1个黑球,共有 ![]() 种取法.显然
种取法.显然 ![]() ,即有等式:
,即有等式: ![]() 成立.试根据上述思想化简下列式子:
成立.试根据上述思想化简下列式子: ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(t)是某港口水的深度y(米)关于时间t(小时)的函数,其中![]() .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 12 | 14.9 | 11.9 | 9 | 12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数![]() 的图象.⑴求
的图象.⑴求![]() 的解析式;⑵设水深不小于
的解析式;⑵设水深不小于![]() 米时,轮船才能进出港口。某轮船在一昼夜内要进港口靠岸办事,然后再出港。问该轮船最多能在港口停靠多长时间?
米时,轮船才能进出港口。某轮船在一昼夜内要进港口靠岸办事,然后再出港。问该轮船最多能在港口停靠多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},a1=2,a2=6,且满足![]() =2(n≥2且n∈N+)
=2(n≥2且n∈N+)
(1)证明:新数列{an+1-an}是等差数列,并求出an的通项公式
(2)令bn=![]() ,设数列{bn}的前n项和为Sn,证明:S2n-Sn<5
,设数列{bn}的前n项和为Sn,证明:S2n-Sn<5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com