
如图,F1,F2是双曲线C: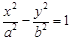 (a>0,b>0)的左、右焦点,过F1的直线与
(a>0,b>0)的左、右焦点,过F1的直线与 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
A.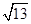 | B.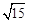 |
| C.2 | D.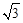 |
A
解析试题分析:∵| AB | : | BF2 | : | AF2 |=3:4 : 5,不妨令|AB|=3,| BF2 | =4,|AF2|=5,
∵|AB|2+ | BF2 | 2=|AF2|2,∴∠ABF2=90°,又由双曲线的定义得:|BF1|-|BF2|=2a,|AF2|-|AF1|=2a,
∴|AF1|+3-4=5-|AF1|,∴|AF1|=3.∴|BF1|-|BF2|=3+3-4=2a,∴a=1.
在Rt△BF1F2中,|F1F2|2=|BF1|2+|BF2|2=62+42=52,又|F1F2|2=4c2,∴4c2=52,∴c=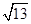 .
.
∴双曲线的离心率e=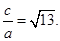
考点:本小题主要考查双曲线的几何性质.
点评:本题考查转化思想与运算能力,其中求得a与c的值是关键,属于中档题


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:单选题
动点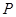 到两定点
到两定点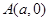 ,
,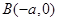 连线的斜率的乘积为
连线的斜率的乘积为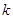 (
(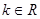 ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
| A.①⑤ | B.③④⑤ | C.①②③⑤ | D.①②③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知双曲线的右焦点F(2,0),设A,B为双曲线上关于原点对称的两点,以AB为直径的圆过点F,直线AB的斜率为 ,则双曲线的的离心率为( )
,则双曲线的的离心率为( )
A. | B. | C.4 | D.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com