
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
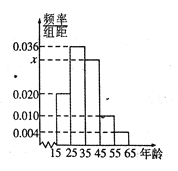
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
【答案】(1)![]() ,
,![]() ,30;(2)第1组2人,第2组3人,第3组1人;(3)
,30;(2)第1组2人,第2组3人,第3组1人;(3)![]() .
.
【解析】试题分析:(1)直接利用频率分布直方图,结合累积频率为1,频数=频率×样本容量,可分别求出![]() 和
和![]() 的值,最高点的中点横坐标即为众数;
的值,最高点的中点横坐标即为众数;
(2)直接利用抽样比即可求第1,2,3组每组各抽取人数.
(3)列出(2)抽取的6人中随机抽取2人是所有情况,求出这2人来自同一个组的数目,即可求解概率.
试题解析:
(1)由题意可知,![]() ,
,
由![]() ,
,
解得![]() ,
,
由频率分布直方图可估计这组数据的众数为30;
(2)第1,3,4组频率之比为0.020:0.030:0.010=2:3:1
则从第1组抽取的人数为![]() ,
,
从第3组抽取的人数为![]() ,
,
从第4组抽取的人数为![]() ;
;
(3)设第1组抽取的2人为![]() ,第3组抽取的3人为
,第3组抽取的3人为![]() ,第4组抽取的1人为
,第4组抽取的1人为![]() ,则从这6人中随机抽取2人有如下种情形:
,则从这6人中随机抽取2人有如下种情形:![]() ,
,
![]() ,共有15个基本事件.
,共有15个基本事件.
其中符合“抽取的2人来自同一个组”的基本事件有![]() 共4个基本事件,
共4个基本事件,
所以抽取的2人来自同一个组的概率![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在各棱长为![]() 的直四棱柱
的直四棱柱![]() 中,底面
中,底面![]() 为棱形,
为棱形, ![]() 为棱
为棱![]() 上一点,且
上一点,且![]()

(1)求证:平面![]() 平面
平面![]() ;
;
(2)平面![]() 将四棱柱
将四棱柱![]() 分成上、下两部分,求这两部分的体积之比.
分成上、下两部分,求这两部分的体积之比.
(棱台的体积公式为![]() ,其中
,其中![]() 分别为上、下底面面积,
分别为上、下底面面积, ![]() 为棱台的高)
为棱台的高)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 有如下结论:
有如下结论:
①该函数为偶函数;
②若![]() ,则
,则![]() ;
;
③其单调递增区间是![]() ;
;
④值域是![]() ;
;
⑤该函数的图象与直线![]() 有且只有一个公共点.(本题中
有且只有一个公共点.(本题中![]() 是自然对数的底数)
是自然对数的底数)
其中正确的是__________.(请把正确结论的序号填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
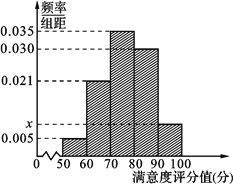
(1) 求图中![]() 的值;
的值;
(2) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com