
分析 通过直线l过点M(1,1)可设其方程为x=m(y-1)+1,并与椭圆方程联立,利用韦达定理及中点坐标公式计算即得结论.
解答 解:依题意,设直线l方程为:x=m(y-1)+1,
联立$\left\{\begin{array}{l}{x=m(y-1)+1}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消去x整理得:
(3+m2)y2-2m(m-1)y+m2-2m-8=0,
设A(x1,y1),B(x2,y2),则y1+y2=$\frac{2m(m-1)}{3+{m}^{2}}$,
∵且线段AB的中点为M(1,1),
∴$\frac{2m(m-1)}{3+{m}^{2}}$=2,即m=-3,
∴直线l方程为x=-3(y-1)+1,即x+3y-4=0,
故答案为:x+3y-4=0.
点评 本题考查直线与圆锥曲线的关系,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{10}-\frac{y^2}{10}$=1 | B. | $\frac{y^2}{10}-\frac{x^2}{10}$=1 | C. | $\frac{x^2}{8}-\frac{y^2}{8}$=1 | D. | $\frac{y^2}{8}-\frac{x^2}{8}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (-1,1) | C. | (0,1) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
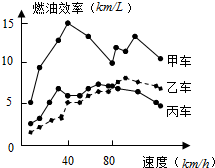 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | [-1,2) | C. | [0,3) | D. | [0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
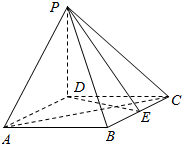 如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com