
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各级城市的大街小巷,为了解我市的市民对共享单车的满意度,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了50人进行分析.若得分低于60分,说明不满意,若得分不低于60分,说明满意,调查满意度得分情况结果用茎叶图表示如图1.
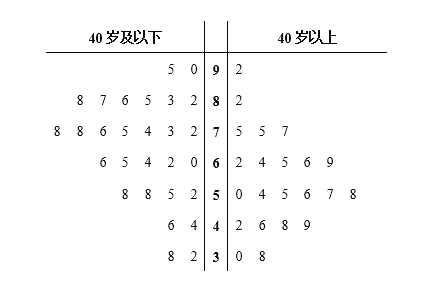
(Ⅰ)根据茎叶图找出40岁以上网友中满意度得分的众数和中位数;
(Ⅱ)根据茎叶图完成下面列联表,并根据以上数据,判断是否有![]() 的把握认为满意度与年龄有关;
的把握认为满意度与年龄有关;
满意 | 不满意 | 合计 | |
40岁以下 | |||
40岁以上 | |||
合计 |
(Ⅲ)先采用分层抽样的方法从40岁及以下的网友中选取7人,再从这7人中随机选出2人,将频率视为概率,求选出的2人中至少有1人是不满意的概率.
参考格式: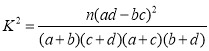 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(Ⅰ)众数为75,中位数为57.5;(Ⅱ)见解析,没有![]() 的把握认为满意度与年龄有关;(Ⅲ)
的把握认为满意度与年龄有关;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由茎叶图直接得出众数,由于40岁以上网友中满意度得分人数为偶数,计算中位数时取平均数。
(Ⅱ)根据题设信息先完成![]() 列联表,再计算
列联表,再计算![]() ,查表确定是否有
,查表确定是否有![]() 的把握认为满意度与年龄有关.
的把握认为满意度与年龄有关.
(Ⅲ)根据分层抽样要求,确定出抽取7人的满意情况,列出所有随机选出2人的基本事件,根据古典概型概率公式求出选出的2人中至少有1人是不满意的概率.
解:(Ⅰ)由题意可得,40岁以上网友中满意度得分的众数为75,中位数为![]() .
.
(Ⅱ)由茎叶图可得![]() 列联表如下:
列联表如下:
满意 | 不满意 | 合计 | |
40岁以下 | 20 | 8 | 28 |
40岁以上 | 10 | 12 | 22 |
合计 | 30 | 20 | 50 |
可知![]()
所以没有![]() 的把握认为满意度与年龄有关.
的把握认为满意度与年龄有关.
(Ⅲ)从所选取的40岁以下的网友中,采用分层抽样的方法选取7人,其中满意度为满意的有5人,分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,不满意的有2人,
,不满意的有2人,
分别为![]() ,
,![]() , 所有组合的情况为
, 所有组合的情况为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,共有21种.
,共有21种.
其中选出的2人中至少有1人是不满意的有11种,
故所求的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式.在某市,随机调查了200名顾客购物时使用手机支付的情况,得到如下的2×2列联表,已知从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(I)根据已知条件完成2×2列联表,并根据此资料判断是否有99.5%的把握认为“市场购物用手机支付与年龄有关”?
2×2列联表:
青年 | 中老年 | 合计 | |
使用手机支付 | 120 | ||
不使用手机支付 | 48 | ||
合计 | 200 |
(Ⅱ)现采用分层抽样的方法从这200名顾客中按照“使用手机支付”和“不使用手机支付”抽取一个容量为10的样本,再从中随机抽取3人,求这三人中“使用手机支付”的人数的分布列及期望.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位全体650人中采用分层抽样的办法抽取50人进行问卷调查,得到了如下列联表:
喜欢户外运动 | 不喜欢户外运动 | 总计 | |
男性 | 5 | ||
女性 | 10 | ||
总计 | 50 |
已知在这50人中随机抽取1人,抽到喜欢户外运动的员工的概率是![]() .
.
(1)请将上面的列联表补充完整;
(2)求该公司男、女员工各多少人;
(3)在犯错误的概率不超过0.005的前提下能否认为喜欢户外运动与性别有关?并说明你的理由.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: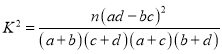 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是函数
是函数![]() 的极值点,求函数
的极值点,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(3)在(2)的条件下,是否存在实数![]() ,使得函数
,使得函数![]() 的图象与函数
的图象与函数![]() 的图象恰有
的图象恰有![]() 个交点?若存在,请求出
个交点?若存在,请求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com