
为保护我国的稀土资源,国家限定某矿区的出口总量不能超过80吨,该矿区计划从2006年开始出口,当年出口a吨,以后每一年出口量均比上一年减少10%.
(Ⅰ)以2006年为第一年,设第n年出口量为an吨,试求an.
(Ⅱ)因稀土资源不能再生,国家计划10年后终止该矿区的出口,问2006年最多出口多少吨?(保留一位小数)参考数据:0.910≈0.35.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(文)对于数列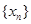 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为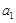 ,公差为
,公差为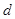 的无穷等差数列
的无穷等差数列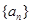 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项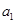 ,第三项
,第三项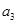 和第五项
和第五项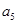 .
.
(1) 若 成等比数列,求
成等比数列,求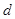 的值;
的值;
(2) 在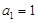 ,
, 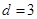 的无穷等差数列
的无穷等差数列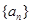 中,是否存在无穷子数列
中,是否存在无穷子数列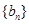 ,使得数列
,使得数列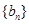 为等比数列?若存在,请给出数列
为等比数列?若存在,请给出数列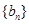 的通项公式并证明;若不存在,说明理由;
的通项公式并证明;若不存在,说明理由;
(3) 他在研究过程中猜想了一个命题:“对于首项为正整数 ,公比为正整数
,公比为正整数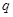 (
(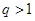 )的无穷等比数 列
)的无穷等比数 列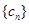 ,总可以找到一个子数列
,总可以找到一个子数列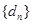 ,使得
,使得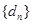 构成等差数列”. 于是,他在数列
构成等差数列”. 于是,他在数列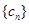 中任取三项
中任取三项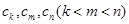 ,由
,由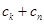 与
与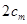 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0—1三角数表.从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第 次全行的数都为1的是第 行.
次全行的数都为1的是第 行.
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
…………
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com