练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数h(x)＝(m2－5m＋1)xm+1为幂函数，且为奇函数．

    (I)求m的值；

    (II)求函数g(x)＝h(x)＋，x∈的值域．

    【答案】（1）m＝0（2）

    【解析】试题分析：（1）根据幂函数定义得m2－5m＋1＝1，解得m＝0或5，再根据幂函数为奇函数得m＝0（2）换元将函数化为一元二次函数，结合自变量取值范围与定义区间位置关系确定函数最值，得函数值域

    试题解析：解：(1)∵函数h(x)＝(m2－5m＋1)xm＋1为幂函数，∴m2－5m＋1＝1，.

    解得m＝0或5

    又h(x)为奇函数，∴m＝0

    (2)由(1)可知g(x)＝x＋，x∈，

    令＝t，则x＝－t2＋，t∈[0,1]，

    ∴f(t)＝－t2＋t＋＝－ (t－1)2＋1∈，故g(x)＝h(x)＋，x∈的值域为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】三国魏人刘徽，自撰《海岛算经》，专论测高望远。其中有一题：今有望海岛，立两表齐，高三丈，前后相去千步，令后表与前表相直。从前表却行一百二十三步，人目著地取望岛峰，与表末参合。从后表却行百二十七步，人目著地取望岛峰，亦与表末参合。问岛高及去表各几何？ 译文如下：要测量海岛上一座山峰的高度，立两根高均为丈的标杆和，前后标杆相距步，使后标杆杆脚与前标杆杆脚与山峰脚在同一直线上，从前标杆杆脚退行步到，人眼著地观测到岛峰，、、三点共线，从后标杆杆脚退行步到，人眼著地观测到岛峰，、、三点也共线，问岛峰的高度 步． （古制：步=尺，里=丈=尺=步）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数把的图象向右平移个单位后，图象恰好为函数的图象，则的值可以是( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量（单位：台），并根据这10个卖场的销售情况，得到如图所示的茎叶图. 为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”．

    （1）求在这10个卖场中，甲型号电视机的“星级卖场”的个数；

    （2）若在这10个卖场中，乙型号电视机销售量的平均数为26.7，求a>b的概率；

    （3）若a=1，记乙型号电视机销售量的方差为，根据茎叶图推断b为何值时，达到最值．

    （只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.

    (1)求 (2)证明:

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(1) 若函数f(x)＝|4x－x2|＋a有4个零点，求实数a的取值范围；

    (2) 已知函数f(x)＝x2＋2mx＋3m＋4.

    ① 若函数f(x)有且仅有一个零点，求实数m的值；

    若函数f(x)有两个零点且两个零点均比－1大，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心是坐标原点，焦点在轴上，离心率为，又椭圆上任一点到两焦点的距离和为．过右焦点与轴不垂直的直线交椭圆于，两点．

    （1）求椭圆的方程；

    （2）在线段上是否存在点，使得？若存在，求出的取值范围；若不存在，请

    说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】统计表明，某种型号的汽车在匀速行驶中每小时耗油量（升）关于行驶速度（千米/小时）的函数解析式可以表示为： ，已知甲、乙两地相距100千米．

    （1）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？

    （2）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的参数方程为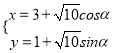（为参数），以直角坐标系原点为极点，以轴正半轴为极轴，建立极坐标系.

    （1）求曲线的极坐标方程，并说明其表示什么轨迹；

    （2）若直线的极坐标方程为，求直线被曲线截得的弦长.

    查看答案和解析>>

    同步练习册答案