
【题目】有编号为1,2,3…n的n个学生,入座编号为1,2,3…n的n个座位,每个学生规定坐一个座位, 设学生所坐的座位号与该生的编号不同的学生人数为![]() , 已知
, 已知![]() 时, 共有6种坐法.
时, 共有6种坐法.
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的概率分布列及数学期望
的概率分布列及数学期望![]() .
.
【答案】(1)![]() ;(2)分布列详见解析,
;(2)分布列详见解析,![]() .
.
【解析】
试题(1)解题的关键是ξ=2时,共有6种坐法,写出关于n的表示式,解出未知量,把不合题意的舍去.
(2)学生所坐的座位号与该生的编号不同的学生人数为ξ,由题意知ξ的可能取值是0,2,3,4,当变量是0时表示学生所坐的座位号与该生的编号都相同,当变量是2时表示学生所坐的座位号与该生的编号有2个相同,理解变量对应的事件,写出分布列和期望.
解:(1)∵当ξ=2时,有Cn2种坐法,
∴Cn2=6,
即![]() ,
,
n2﹣n﹣12=0,n=4或n=﹣3(舍去),
∴n=4.
(2)∵学生所坐的座位号与该生的编号不同的学生人数为ξ,
由题意知ξ的可能取值是0,2,3,4,
当变量是0时表示学生所坐的座位号与该生的编号都相同,
当变量是2时表示学生所坐的座位号与该生的编号有2个相同,
当变量是3时表示学生所坐的座位号与该生的编号有1个相同,
当变量是4时表示学生所坐的座位号与该生的编号有0个相同,
∴![]() ,
,
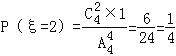 ,
,
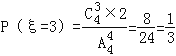 ,
,
![]() ,
,
∴ξ的概率分布列为:
ξ | 0 | 2 | 3 | 4 |
P |
|
|
|
|
∴![]() .
.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=2x和g(x)=2x的图象如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.

(1)请指出图中曲线C1,C2分别对应的函数;
(2)结合函数图象,判断![]() 与
与![]() ,f(2 019)与g(2 019)的大小.
,f(2 019)与g(2 019)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位用2160万元购得一块空地,计划在该空地上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=购地总费用/建筑总面积)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 既有一个极小值又有一个极大值,求
既有一个极小值又有一个极大值,求![]() 的取值范围;
的取值范围;
(3)若存在![]() ,使得当
,使得当![]() 时,
时, ![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高玉米产量,某种植基地对单位面积播种数与每棵作物的产量之间的关系进行了研究,收集了![]() 块试验田的数据,得到下表:
块试验田的数据,得到下表:
试验田编号 |
|
|
|
|
|
|
|
|
|
|
|
(棵/) |
|
|
|
|
|
|
|
|
|
|
|
(斤/棵) |
|
|
|
|
|
|
|
|
|
|
|
技术人员选择模型![]() 作为
作为![]() 与
与![]() 的回归方程类型,令
的回归方程类型,令![]() ,
,![]() 相关统计量的值如下表:
相关统计量的值如下表:
|
|
|
|
|
|
|
|
由表中数据得到回归方程后进行残差分析,残差图如图所示:

(1)根据残差图发现一个可疑数据,请写出可疑数据的编号(给出判断即可,不必说明理由);
(2)剔除可疑数据后,由最小二乘法得到关于的线性回归方程![]() 中的
中的![]() ,求
,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)利用(2)得出的结果,计算当单位面积播种数![]() 为何值时,单位面积的总产量
为何值时,单位面积的总产量![]() 的预报值最大?(计算结果精确到
的预报值最大?(计算结果精确到![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为 ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据市场调查,某种商品一年内每件出厂价在6千元的基础上,按月呈![]() 的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,该商品每件的售价为
的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,该商品每件的售价为![]() (x为月份),且满足
(x为月份),且满足![]() .
.
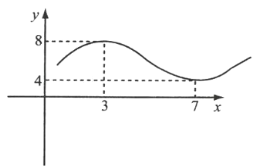
(1)分别写出该商品每件的出厂价函数![]() 和售价函数
和售价函数![]() 的解析式;
的解析式;
(2)问几月份的销售盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,以
,以![]() 为圆心的圆记为圆
为圆心的圆记为圆![]() ,已知圆
,已知圆![]() 上的点与圆
上的点与圆![]() 上的点之间距离的最大值为21.
上的点之间距离的最大值为21.
(1)求圆![]() 的标准方程;
的标准方程;
(2)求过点![]() 且与圆
且与圆![]() 相切的直线的方程;
相切的直线的方程;
(3)已知直线![]() 与
与![]() 轴不垂直,且与圆
轴不垂直,且与圆![]() ,圆
,圆![]() 都相交,记直线
都相交,记直线![]() 被圆
被圆![]() ,圆
,圆![]() 截得的弦长分别为
截得的弦长分别为![]() ,
,![]() .若
.若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com