
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 根据题意,求出数列{an}的通项公式,得出它的前n项和公式,计算$\frac{{S}_{4}}{{S}_{2}}$的值即可.
解答 解:∵数列{log2an}是公差为1的等差数列,
∴log2an=log2a1+(n-1),
∴log2$\frac{{a}_{n}}{{a}_{1}}$=n-1,
∴$\frac{{a}_{n}}{{a}_{1}}$=2n-1,
∴an=a1•2n-1;
即数列{an}是公比为2的等比数列,其前n项和为
Sn=$\frac{{a}_{1}(1{-2}^{n})}{1-2}$=(2n-1)•a1,
∴$\frac{{S}_{4}}{{S}_{2}}$=$\frac{{(2}^{4}-1){•a}_{1}}{{(2}^{2}-1){•a}_{1}}$=5.
故选:A.
点评 本题考查了对数的运算性质与等差数列、等比数列的定义和通项公式以及前n项和公式的应用问题,是综合性题目.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80 | B. | 90 | C. | 120 | D. | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4] | B. | [2,4) | C. | [2,4] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
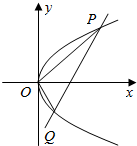 已知抛物线C:y2=2px(p>0)上的点(2,a)到焦点F的距离为3.
已知抛物线C:y2=2px(p>0)上的点(2,a)到焦点F的距离为3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com