
分析 利用直线l:x+my+m=0经过定点,A(0,-1),求得直线AQ的斜率kAQ,直线AP的斜率kAP即可得答案.
解答 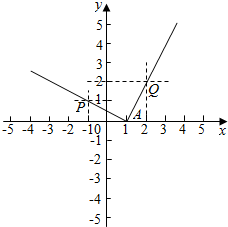 解:直线mx+y-m=0等价为y=-m(x-1)则直线过定点A(1,0),
解:直线mx+y-m=0等价为y=-m(x-1)则直线过定点A(1,0),
作出对应的图象如图:
则由图象可知直线的斜率k=-m,
满足k≥kAQ或k≤kAP,
即-m≥$\frac{2-0}{2-1}$=2或-m≤$\frac{1-0}{-1-1}$=-$\frac{1}{2}$,
则m≤-2或m≥$\frac{1}{2}$,
故答案为:m≤-2或m≥$\frac{1}{2}$.
点评 本题考查:两条直线的交点坐标,考查恒过定点的直线,考查直线的斜率的应用,考查作图与识图能力,属于中档题.


科目:高中数学 来源: 题型:选择题
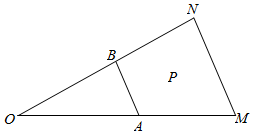 如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )
如图,在△OMN中,A,B分别是OM,ON中点,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R),且点P落在四边形ABNM内(含边界),则x2+y2的取值范围是( )| A. | [1,2] | B. | [1,4] | C. | $[\frac{1}{2},1]$ | D. | $[\frac{1}{2},4]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
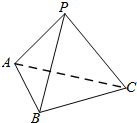 如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.
如图在三棱锥P-ABC中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为$\frac{9}{2}π$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com