
分析 (1)利用二倍角公式以及两角和与差的三角函数化简函数的解析式,然后求解振幅、周期和初相.
(2)利用正弦函数的最值,直接求解即可.
解答 解:y=$\frac{1}{2}$cos2x+$\frac{{\sqrt{3}}}{2}$sinxcosx+1=$\frac{1}{4}$cos2x+$\frac{{\sqrt{3}}}{4}$sin2x+$\frac{5}{4}$…(2分)
=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)+$\frac{5}{4}$…(4分)
(1)函数的振幅为A=$\frac{1}{2}$,周期为T=$\frac{2π}{2}$=π,初相为φ=$\frac{π}{6}$…(8分)
(2)函数的最大值是$\frac{1}{2}$+$\frac{5}{4}$=$\frac{7}{4}$,此时2x+$\frac{π}{6}$=$\frac{π}{2}$+2kπ,x=$\frac{π}{6}$+kπ,k∈Z…(10分)
函数的最小值是$-\frac{1}{2}$+$\frac{5}{4}$=$\frac{3}{4}$,此时2x+$\frac{π}{6}$=$-\frac{π}{2}$+2kπ,x=$-\frac{π}{3}$+kπ,k∈Z…(12分)
点评 本题考查两角和与差的三角函数,二倍角公式的应用,三角函数的简单性质的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
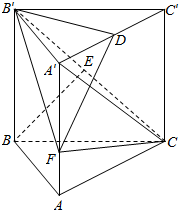 如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
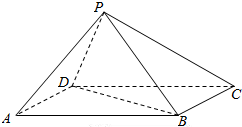 如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.
如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com