
【题目】已知函数![]() ,在区间
,在区间![]() 内任取两个实数
内任取两个实数![]() ,且
,且![]() ,若不等式
,若不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】一张半径为4的圆形纸片的圆心为![]() ,
, ![]() 是圆内一个定点,且
是圆内一个定点,且![]() ,
, ![]() 是圆上一个动点,把纸片折叠使得
是圆上一个动点,把纸片折叠使得![]() 与
与![]() 重合,然后抹平纸片,折痕为
重合,然后抹平纸片,折痕为![]() ,设
,设![]() 与半径
与半径![]() 的交点为
的交点为![]() ,当
,当![]() 在圆上运动时,则
在圆上运动时,则![]() 点的轨迹为曲线
点的轨迹为曲线![]() ,以
,以![]() 所在直线
所在直线![]() 为轴,
为轴, ![]() 的中垂线为
的中垂线为![]() 轴建立平面直角坐标系,如图.
轴建立平面直角坐标系,如图.
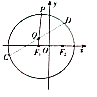
(1)求曲线![]() 的方程;
的方程;
(2)曲线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴不重合的动直线
轴不重合的动直线![]() 过点
过点![]() 且与
且与![]() 交于
交于![]() 、
、![]() 两点(其中
两点(其中![]() 在
在![]() 轴上方),设直线
轴上方),设直线![]() 、
、![]() 交于点
交于点![]() ,求证:动点
,求证:动点![]() 恒在定直线
恒在定直线![]() 上,并求
上,并求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.下图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知![]() ,历年中日泄流量在区间[30,60)
,历年中日泄流量在区间[30,60)
的年平均天数为156,一年按364天计.
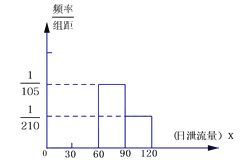
(Ⅰ)请把频率分布直方图补充完整;
(Ⅱ)该水电站希望安装的发电机尽可能运行,但每30万立方米的日泄流量才够运行一台发电机,如![]() 时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
A小区 | 低碳族 | 非低碳族 |
比例 |
|
|
B小区 | 低碳族 | 非低碳族 |
比例 |
|
|
C小区 | 低碳族 | 非低碳族 |
比例 |
|
|
(1)从A,B,C三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将数列
,则将数列![]() 和
和![]() 的距离定义为
的距离定义为![]() .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,数列
的集合,数列![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() .若
.若![]() ,
, ![]() ,数列
,数列![]() 和
和![]() 的距离小于2016,求
的距离小于2016,求![]() 的最大值.
的最大值.
(3)记![]() 是所有7项数列
是所有7项数列![]() (其中
(其中![]() ,
, ![]() 或
或![]() )的集合,
)的集合, ![]() ,且
,且![]() 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: ![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com