
【题目】约公元前600年,几何学家泰勒斯第一个测出了金字塔的高度.如图,金字塔是正四棱锥,泰勒斯先测量出某个金字塔的底棱长约为230米;然后,他站立在沙地上,请人不断测量他的影子,当他的影子和身高相等时,他立刻测量出该金字塔影子的顶点A与相应底棱中点B的距离约为22.2米.此时,影子的顶点A和底面中心O的连线恰好与相应的底棱垂直,则该金字塔的高度约为( )
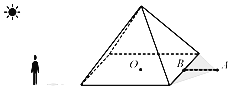
A.115米B.137.2米C.230米D.252.2米
科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
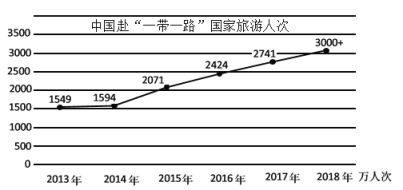
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2014年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①②③B.②③C.①②D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是梯形,
是梯形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
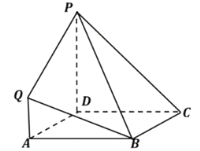
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知点![]() 在棱
在棱![]() 上,且异面直线
上,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎COVID-19疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,小王同学发现,每个国家在疫情发生的初期,由于认识不足和措施不到位,感染人数都会出现快速的增长.下表是小王同学记录的某国连续8天每日新型冠状病毒感染确诊的累计人数.
日期代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累计确诊人数y | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
为了分析该国累计感染人数的变化趋势,小王同学打算从①![]() ,②
,②![]() 中选择一种模型对变量x和y的关系进行拟合,得到相应的回归方程,经过计算得
中选择一种模型对变量x和y的关系进行拟合,得到相应的回归方程,经过计算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
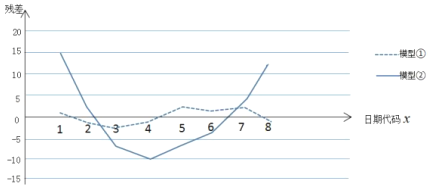
(1)请根据散点图,比较模型①,②的拟合效果,小王应该选择哪个模型?
(2)根据(1)问选定的模型求出相应的回归方程(系数均保留一位小数);
(3)由于时差,该国截止第9天新型冠状病毒感染确诊的累计人数尚未公布.小王同学认为,如果防疫形势没有得到明显改善,在数据公布之前可以根据他在(2)问求出的回归方程来对感染人数作出预测,那么估计该地区第9天新型冠状病毒感染确诊的累计人数是多少.
附:回归直线的最小二乘估计参考公式为: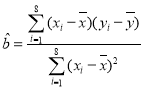 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
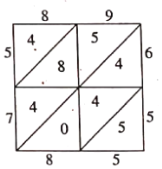
【题目】写算,是一种格子乘法,也是笔算乘法的一种,用以区别筹算与珠算,它由明代数学家吴敬在其撰写的《九章算法比类大全》一书中提出,是从天元式的乘法演变而来.例如计算![]() ,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出
,将被乘数89计入上行,乘数65计入右行.然后以乘数65的每位数字乘被乘数89的每位数字,将结果计入相应的格子中,最后从右下方开始按斜行加起来,满十向上斜行进一,如图,即得5785.类比此法画出![]() 的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
的表格,若从表内(表周边数据不算在内)任取一数,则恰取到奇数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com