练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．求函数y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+1}}$的最小值．

    分析 设x2+1=t，则t≥1，在利用导数和函数的最值得关系即可求出答案

    解答 解：设x2+1=t，则t≥1，
    ∴y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+1}}$=$\sqrt{t+1}$+$\frac{1}{\sqrt{t}}$，t≥1，
    ∴y′=$\frac{1}{2}$$（t+1）^{-\frac{1}{2}}$-$\frac{1}{2}$${t}^{-\frac{3}{2}}$=$\frac{1}{2}$（$\frac{1}{\sqrt{t+1}}$-$\frac{1}{t\sqrt{t}}$）＞0，
    ∴函数y=$\sqrt{t+1}$+$\frac{1}{\sqrt{t}}$在[1，+∞）为增函数，
    ∴当t=1时，函数有最小值，
    ∴ymin=$\sqrt{2}$+1．

    点评 本题考查了函数的单调性和函数最值得问题，关键是求导，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知抛物线y2=8x，过点P（2，0）作倾斜角为α的直线l，直线l与抛物线交于A、B两点．
    （1）当α=45°时，写出直线l的参数方程；
    （2）当α=45°时，求线段AB的中点M到点P的距离和中点M的坐标；
    （3）若α为任意角，求2（$\frac{1}{|AP|}$+$\frac{1}{|BP|}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知sinθ=-$\frac{1}{3}$，θ∈（-$\frac{π}{2}$，$\frac{π}{2}$），则sin（θ-5π）•sin（$\frac{3π}{2}$-θ）的值是-$\frac{2\sqrt{2}}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．“光盘行动”倡导厉行节约，反对铺张浪费，带动大家珍惜粮食，吃光盘子中的食物，得到从中央到民众的支持，为了解某地响应“光盘行动”的实际情况，某校几位同学组成研究性学习小组，从某社区[25，55]岁的人群中随机抽取n人进行了一次调查，得到如下统计表：
    组数分组频数频率“光盘族”占本组比例
    第1组[25，30）500.0530%
    第2组[30，35）1000.1030%
    第3组[35，40）1500.1540%
    第4组[40，45）2000.2050%
    第5组[45，50）ab65%
    第6组[50，55）2000.2060%
    （Ⅰ）求a，b的值，并估计本社区[25，55]岁的人群中“光盘族”所占比例；
    （Ⅱ）从年龄段在[35，40）与[40，45）的“光盘族”中，采用分层抽样方法抽取8人参加节约粮食宣传活动，并从这8人中选取2人作为领队．
    （i）已知选取2人中1人来自[35，40）中的前提下，求另一人来自年龄段[40，45）中的概率；
    （ii）求2名领队的年龄之和的期望值（每个年龄段以中间值计算）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．求不等式（ax-1）（x+2）＜0（-$\frac{1}{2}$＜a≤0）的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知关于x的不等式2x2+（3a-7）x+3+a-2a2＞0的解集为A．
    （1）若0∈A，求a的取值集合；
    （2）在（1）中，若a∈Z，求A．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

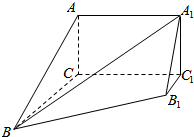    6．如图，几何体ABC-A1B1C1中，平面ABC∥平面A1B1C1，平面ACC1A1为矩形，平面ACC1A1⊥平面BCC1B1，已知AC=3，BC=AA1=4，BB1=5，B1C1=1
    （Ⅰ）若平面AA1B∩平面BCC1B1=l，求证：l∥CC1；
    （Ⅱ）求钝二面角A-A1B-B1的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知直线l：$\left\{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}\right.$（t为参数，α为l的倾斜角，且0＜α＜π）与曲线C：$\left\{\begin{array}{l}{x=\sqrt{2}cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）相交于A、B两点，点F的坐标为（1，0）．
    （1）求△ABF的周长；
    （2）若点E（-1，0）恰为线段AB的三等分点，求△ABF的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．在如图所示的边长为2的正方形中随机掷一粒豆子，豆子落在正方形内切圆的上半圆（图中阴影部分）中的概率是（　　）
    A．$\frac{π}{4}$B．$\frac{π}{8}$C．$\frac{1}{4}$D．$\frac{1}{8}$

    查看答案和解析>>

    同步练习册答案