
���� ��1������C�м����귽�̣�ֱ�����ü������ֱ�����껥����ʽ���д������ɣ�
��2�����ȣ�����ֱ�ߵIJ������̣�Ȼ����ȥ���������ɵõ���ͨ���̣�Ȼ��д�ɼ�������ʽ���ɣ�
��3�������������C�ϵ�һ�㣬Ȼ����õ㵽ֱ�ߵľ��룬Ȼ�����ڼнǽ�����⣮
��� �⣺��1��������C�ļ����귽����C��$\frac{4}{{��}^{2}}$=cos2��+4sin2�ȣ�
���2cos2��+4��2sin2��=4��
��x2+4y2=4��
��$\frac{{x}^{2}}{4}+{y}^{2}=1$��
������C����ͨ����Ϊ��$\frac{{x}^{2}}{4}+{y}^{2}=1$��
����ʾһ��������x���ϵ���Բ��
�����������$\left\{\begin{array}{l}{x=2cos��}\\{y=sin��}\end{array}\right.$��
��2����ֱ��l�IJ���������l��$\left\{\begin{array}{l}{x=\sqrt{5}-2016t}\\{y=\sqrt{5}+2016t}\end{array}\right.$
��x+y-2$\sqrt{5}$=0��
��Ӧ�ļ����귽��Ϊ��
��cos��+��sin��-2$\sqrt{5}$=0��
��$\sqrt{2}$��cos����-$\frac{��}{4}$��=2$\sqrt{5}$��
���cos����-$\frac{��}{4}$��=$\sqrt{10}$��
��3����l��x+y-2$\sqrt{5}$=0��
����б��Ϊk=-1��
���P��x��y��Ϊ��Բ������һ�㣬��
��P��ֱ�ߵľ���Ϊd=$\frac{|x+y-2\sqrt{5}|}{\sqrt{2}}$
=$\frac{|2cos��+sin��-2\sqrt{5}|}{\sqrt{2}}$
=$\frac{|\sqrt{5}cos����-����-2\sqrt{5}|}{\sqrt{2}}$��
��dmax=$\frac{3\sqrt{10}}{2}$��dmin=$\frac{\sqrt{10}}{2}$��
��ֱ��MN��ֱ��l�ļнǵ���45�㣬
��|MN|max=$\frac{3\sqrt{10}}{2}��\sqrt{2}=3\sqrt{5}$��
|MN|min=$\frac{\sqrt{10}}{2}��\sqrt{2}=\sqrt{5}$��
���� �����ص㿼�������ߵIJ������̺���ͨ���̵Ļ��������ߵ�ֱ�����귽�̺ͼ����귽�̵Ļ�����ֱ������Բ��λ�ù�ϵ��֪ʶ�������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 22 | C�� | 26 | D�� | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��㶫����ʦ���и����ۺϲ���һ��ѧ���ģ��Ծ��������棩 ���ͣ������
ѡ��4��1������֤��ѡ����
��ͼ��ֱ��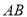 ��Բ��
��Բ��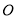 ����Բ
����Բ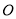 ��
��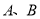 ��ֱ��
��ֱ��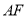 ��Բ
��Բ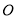 ��
��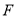 ������
������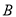 �غϣ���ֱ��
�غϣ���ֱ��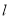 ��Բ
��Բ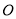 ������
������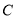 ����
����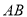 ��
��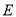 ������
������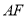 ��ֱ������Ϊ
��ֱ������Ϊ ������
������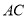 ��
��
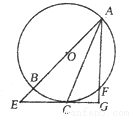
��֤����1��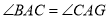 ��
��
��2��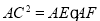 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-6��6�� | B�� | [-6��6] | C�� | ��-�ޣ�-6]��[6��+�ޣ� | D�� | ��-�ޣ�-6���ȣ�6��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com