
【题目】函数f(x)的定义域为(﹣∞,a)∪(a,+∞),f(x)≥0的解集为M,f(x)<0的解集为N,则下列结论正确的是( )
A.M=CRN
B.CRM∩CRN=
C.M∪N=R
D.CRM∪CRN=R
【答案】D
【解析】设A=(﹣∞,a)∪(a,+∞),根据题意得:M∪N=A,M∩N=,
则M=CRACRN,选项A错误;
而CRM∩CRN=CR(M∪N)=CRA={a},选项B错误;
则M∪N=A,选项C错误;
则CRM∪CRN=CR(M∩N)=R,选项D正确,
故选D
【考点精析】关于本题考查的函数的定义域及其求法,需要了解求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能得出正确答案.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
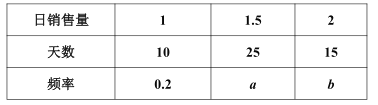
若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的日销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元, ![]() 表示该种商品某两天销售利润的和(单位:千元),求
表示该种商品某两天销售利润的和(单位:千元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在(﹣∞,0)∪(0,+∞)上的偶函数,当x>0时, ![]() .
.
(1)求f(x)的解析式;
(2)讨论函数f(x)的单调性,并求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=ax3﹣x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA , 0)(xA>0); 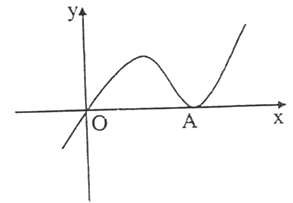
(1)用反证法证明常数c≠0;
(2)如果 ![]() ,求函数的解析式.
,求函数的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“莞马”活动中的α机器人一度成为新闻热点,为检测其质量,从一生产流水线上抽取20件该产品,其中合格产品有15件,不合格的产品有5件.
(1)现从这20件产品中任意抽取2件,记不合格的产品数为X,求X的分布列及数学期望;
(2)用频率估计概率,现从流水线中任意抽取三个机器人,记ξ为合格机器人与不合格机器人的件数差的绝对值,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在点(1,2)处的切线与f(x)的图象有三个公共点,则b的取值范围是( )
在点(1,2)处的切线与f(x)的图象有三个公共点,则b的取值范围是( )
A.[﹣8,﹣4+2 ![]() )
)
B.(﹣4﹣2 ![]() ,﹣4+2
,﹣4+2 ![]() )
)
C.(﹣4+2 ![]() ,8]
,8]
D.(﹣4﹣2 ![]() ,﹣8]
,﹣8]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com