Question

一重物m用绳悬起(如右图所示),绳的另一端在天花板上,绳长l=0.5 m,重物经推动后,在一水平面内做匀速圆周运动,转速n=1 转/秒,求这时绳和竖直方向所成的角度.(g取10 m/s²)

Answer 1

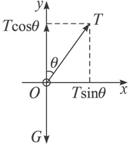
解:重物做匀速圆周运动,加速度是向心加速度,由牛顿第二定律:合外力的方向应与加速度的方向相同.所以,本题中重物所受合外力即绳子拉力T和重力G(大小为mg)的合力f必指向圆心(此即向心力).

在竖直方向上,|T|cosθ=|G|=mg.①

(其中θ为绳与竖直方向成的角)在水平面内,重力所受合力大小|f|=|T|sinθ,

即|T|sinθ=|f|=m|a|.②

(其中a为向心加速度)

由①②得tanθ=.③

圆半径R=lsinθ,圆周长为2πlsinθ,故重物在圆周上的速度大小为|v|=|2πlnsinθ|,④

而|a|==4π²ln²sinθ,

把④代入③得cosθ=.⑤

代入已知数字得cosθ=,故θ=60°.

由⑤可知,物体转速n愈大,θ也愈大.