
分析 (Ⅰ)求出函数的导数,求得切线的斜率和切点,由点斜式方程,可得切线的方程;
(Ⅱ)假设存在m∈($\frac{1}{2}$,1),由F(x)求得导数,求得单调性,可得最小值;再由1+G(x)求得导数,求得单调性,可得最大值,令最小值大于最大值,求得m的范围,即可判断是否存在;
(Ⅲ)根据要证明的结论,利用分析法来证明本题,从结论入手,要证结论只要证明后面这个式子成立,两边取对数,构造函数,问题转化为只要证明函数在一个范围上成立,利用导数证明函数的性质.
解答 解:(Ⅰ)函数f(x)=x-(x+1)ln(x+1)的导数为f′(x)=-ln(x+1),
曲线y=f(x)在x=e-1处的切线斜率为k=-lne=-1,切点为(e-1,-1),
则曲线y=f(x)在x=e-1处的切线方程为y+1=-(x-e+1),
即为x+y-e+2=0;
(Ⅱ)假设存在m∈($\frac{1}{2}$,1),由F(x)=1-mx-$\frac{1+f(x-1)}{x}$=lnx-mx,
F′(x)=$\frac{1}{x}$-m,由x∈[$\frac{1}{e}$,1],可得$\frac{1}{x}$∈[1,e],即有F′(x)>0,
F(x)在[$\frac{1}{e}$,1]上递增,可得x=$\frac{1}{e}$取得最小值为-1-$\frac{m}{e}$;
由1+G(x)=(1-m)x-$\frac{m}{2x}$-2m+1的导数为1-m+$\frac{m}{2{x}^{2}}$>0,
即1+G(x)在[$\frac{1}{e}$,1]上递增,可得x=1时,取得最大值,且为2-$\frac{7m}{2}$.
由假设可得-1-$\frac{m}{e}$>2-$\frac{7m}{2}$.解得m>$\frac{6e}{7e-2}$>$\frac{1}{2}$,
故存在m,且范围是($\frac{6e}{7e-2}$,1);
(Ⅲ)要证:(1+m)n<(1+n)m
只需证nln(1+m)<mln(1+n),
只需证$\frac{ln(1+m)}{m}$<$\frac{ln(1+n)}{n}$,
设g(x)=$\frac{ln(1+x)}{x}$,
则g′(x)=$\frac{x-(1+x)ln(1+x)}{(1+x){x}^{2}}$,
由f(x)=x-(1+x)ln(1+x),导数f′(x)=-ln(x+1),
可得f(x)在(0,+∞)单调递减,
即x>0时,有f(x)<f(0),
∴x-(1+x)ln(1+x)<0,所以g′(x)<0,
即g(x)是(0,+∞)上的减函数,
即当m>n>0时,g(m)<g(n),
故原不等式成立.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用转化思想,考查不等式的证明,注意运用分析法和构造函数,运用单调性,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,1) | C. | (-1,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
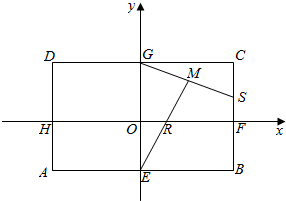 矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.
矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e) | B. | (-e,-1) | C. | (1,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com