
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏, 从中部选择河北. 湖北,从西部选择宁夏, 从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记. 由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验. 在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)以频率作为概率, 某普查小组从该小区随机选择 1 家企事业单位,3 家个体经营户作为普查对象,入户登记顺利的对象数记为![]() , 写出
, 写出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的![]() ,全世界近
,全世界近![]() 人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨):一位居民的月用水量不超过
(吨):一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水不按议价收费,估计
的居民每月的用水不按议价收费,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
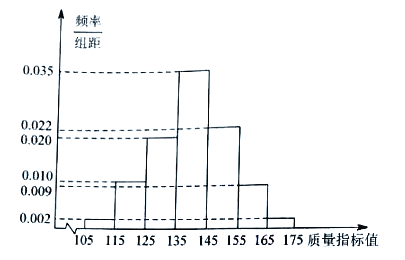
(1)求这1000件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表)
(同一组数据用该区间的中点值作代表)
(2)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中以
,其中以![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ⅱ)某用户从该工厂购买了100件这种产品,记![]() 表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求
表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥S![]() ABC中,
ABC中,![]() ,O为BC的中点.
,O为BC的中点.
(1)求证:![]() 面ABC;
面ABC;
(2)求异面直线![]() 与AB所成角的余弦值;
与AB所成角的余弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ;若存在,求
;若存在,求![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.先把高二年级的![]() 名学生编号:
名学生编号:![]() 到
到![]() ,再从编号为
,再从编号为![]() 到
到![]() 的学生中随机抽取
的学生中随机抽取![]() 名学生,其编号为
名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() 的学生,这种抽样方法是分层抽样法
的学生,这种抽样方法是分层抽样法
B.线性回归直线![]() 不一定过样本中心
不一定过样本中心![]()
C.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于
的值越接近于![]()
D.若一组数据![]() ,
,![]() ,
,![]() ,
,![]() 的平均数是
的平均数是![]() ,则该组数据的方差也是
,则该组数据的方差也是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定直线
到定直线![]() :
:![]() 的距离比到定点
的距离比到定点![]() 的距离大2.
的距离大2.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)在![]() 轴正半轴上,是否存在某个确定的点
轴正半轴上,是否存在某个确定的点![]() ,过该点的动直线
,过该点的动直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,使得
两点,使得![]() 为定值.如果存在,求出点
为定值.如果存在,求出点![]() 坐标;如果不存在,请说明理由.
坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 引圆
引圆![]() 的两条切线
的两条切线![]() ,切线
,切线![]() 与抛物线
与抛物线![]() 的另一交点分别为
的另一交点分别为![]() ,线段
,线段![]() 中点的横坐标记为
中点的横坐标记为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南北朝时期杰出的数学家祖冲之的儿子祖暅在数学上也有很多创造,其最著名的成就是祖暅原理:夹在两个平行平面之间的几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,现有一个圆柱体和一个长方体,它们的底面面积相等,高也相等,若长方体的底面周长为![]() ,圆柱体的体积为
,圆柱体的体积为![]() ,根据祖暅原理,可推断圆柱体的高( )
,根据祖暅原理,可推断圆柱体的高( )
A.有最小值![]() B.有最大值
B.有最大值![]() C.有最小值
C.有最小值![]() D.有最大值
D.有最大值![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com