
在数列{an}中,a1=1,an+1=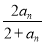 ,n∈N+,求a2,a3,a4
,n∈N+,求a2,a3,a4
并猜想数列的通项公式,并给出证明.
科目:高中数学 来源:2015届辽宁大连普通高中高二上学期期末考试文数学卷(解析版) 题型:解答题
已知离心率 的椭圆
的椭圆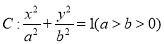 一个焦点为
一个焦点为 .
.
(1)求椭圆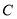 的方程;
的方程;
(2) 若斜率为1的直线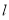 交椭圆
交椭圆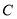 于
于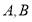 两点,且
两点,且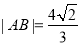 ,求直线
,求直线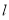 方程.
方程.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.3练习卷(解析版) 题型:解答题
平面内有n(n∈N+,n≥2)条直线,其中任何两条不平行,任何三条不过
同一点,证明:交点的个数f(n)= .
.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.2练习卷(解析版) 题型:选择题
已知a,b,c是三条互不重合的直线,α,β是两个不重合的平面,给出
四个命题:①a∥b,b∥α,则a∥α;②a,b?α,a∥β,b∥β,则α∥β;③a⊥α,a∥β,则α⊥β;④a⊥α,b∥α,则a⊥b.
其中正确的命题个数是 ( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.1练习卷(解析版) 题型:解答题
设V为全体平面向量构成的集合,若映射f:
V→R满足:
对任意向量a=(x1,y1)∈V,b=(x2,y2)∈V,以及任意λ∈R,均有f[λa+(1-λ)b]=λf(a)+(1-λ)f(b),则称映射f具有性质p.
现给出如下映射:
①f1:V→R,f1(m)=x-y,m=(x,y)∈V;
②f2:V→R,f2(m)=x2+y,m=(x,y)∈V;
③f3:V→R,f3(m)=x+y+1,m=(x,y)∈V.
分析映射①②③是否具有性质p.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标6.1练习卷(解析版) 题型:选择题
设n是自然数,则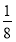 (n2-1)[1-(-1)n]的值 ( )
(n2-1)[1-(-1)n]的值 ( )
A.一定是零 B.不一定是整数
C.一定是偶数 D.是整数但不一定是偶数
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标4章末练习卷(解析版) 题型:选择题
曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的
三角形的面积为 ( ).

A. B.
B. C.
C. D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com